题目内容
设x∈R,[x]表示不大于x的最大整数,如[π]=3, [-1.2]=-2, [
]=0,则使[|x-1|]=3成立的x的取值范围
| 1 | 2 |
(-3,-2]∪[4,5)
(-3,-2]∪[4,5)
.分析:由题意,根据所给的定义可将[|x-1|]=3转化为3≤|x-1|<4,解此绝对值不等式即可求出x的取值范围
解答:解:由题意[|x-1|]=3,则3≤|x-1|<4
∴3≤x-1<4或-4≤x-1<-3
解得4≤x<5或-3<x≤-2
所以使[|x-1|]=3成立的x的取值范围是(-3,-2]∪[4,5)
故答案为(-3,-2]∪[4,5)
∴3≤x-1<4或-4≤x-1<-3
解得4≤x<5或-3<x≤-2
所以使[|x-1|]=3成立的x的取值范围是(-3,-2]∪[4,5)
故答案为(-3,-2]∪[4,5)
点评:本题考查函数定义域的求法,理解题意,得到x所满足的不等式是解本题的关键,本题是一个新定义的题,理解定义是本题的难点,新定义的题由于其考查推理判断能力的优势,在近年的高考试卷上所占的分值逐年加大,要多加重视此类题的解题的规律

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
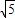 )
)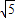 ,-2]
,-2]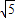 ,-2]∪[2,
,-2]∪[2,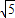 )
)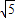 ,-2]∪[2,
,-2]∪[2,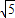 ]
]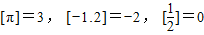 ,则使[|x-1|]=3成立的x的取值范围 .
,则使[|x-1|]=3成立的x的取值范围 . ,则使[|x-1|]=3成立的x的取值范围 .
,则使[|x-1|]=3成立的x的取值范围 .