题目内容
已知函数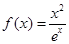 ,
,
(1)求函数 的单调区间;
的单调区间;
(2)若方程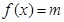 有且只有一个解,求实数m的取值范围;
有且只有一个解,求实数m的取值范围;
(3)当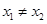 且
且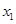 ,
, 时,若有
时,若有 ,求证:
,求证: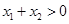 .
.
(1) 的递增区间为
的递增区间为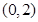 ,递减区间为
,递减区间为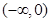 和
和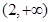 ;(2)
;(2)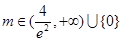 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)对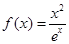 求导可得
求导可得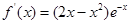 ,令
,令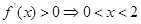 ,
,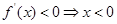 或
或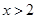 ,由导数与单调性的关系可知,所以
,由导数与单调性的关系可知,所以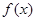 递增区间为
递增区间为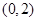 ,递减区间为
,递减区间为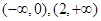 ;
;
(2)若方程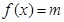 有解
有解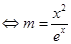 有解,则原问题转化为求f(x)的值域,而m只要在f(x)的值域内即可,由(1)知
有解,则原问题转化为求f(x)的值域,而m只要在f(x)的值域内即可,由(1)知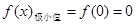 ,
,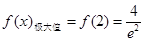 ,
, 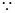 方程
方程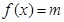 有且只有一个根,又
有且只有一个根,又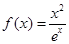 的值域为
的值域为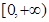 ,
,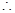
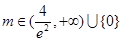 ;
;
(3)由(1)和(2)及当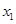 ,
, 时,有
时,有 ,不妨设
,不妨设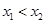 ,
,
则有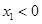 ,
,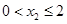 ,又
,又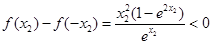 ,
,
即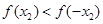 ,同理
,同理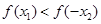 ,又
,又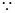
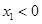 ,
,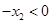 ,且
,且 在
在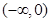 上单调递减,
上单调递减,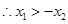 ,即
,即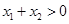 .
.
试题解析:(1)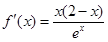 ,令
,令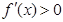 ,即
,即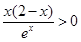 ,解得
,解得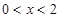 ,
,
令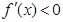 ,即
,即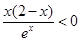 ,解得
,解得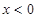 ,或
,或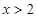 ,
,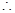
 的递增区间为
的递增区间为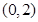 ,递减区间为
,递减区间为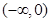 和
和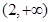 . 4分
. 4分
(2)由(1)知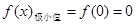 ,
,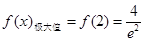 , 6分
, 6分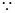 方程
方程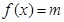 有且只有一个根,又
有且只有一个根,又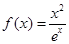 的值域为
的值域为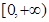 ,由图象知
,由图象知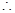
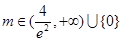 8分
8分
(3)由(1)和(2)及当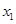 ,
, 时,有
时,有 ,不妨设
,不妨设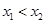 ,
,
则有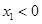 ,
,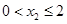 ,又
,又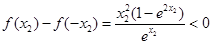 ,
,
即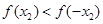 , 11分
, 11分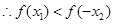 ,又
,又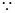
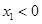 ,
,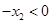 ,且
,且 在<
在<

练习册系列答案
相关题目
 (a为常数).
(a为常数).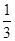 ax3-
ax3- x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.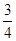 x2-bx+
x2-bx+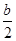 -
- 在
在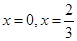 处存在极值.
处存在极值.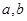 的值;
的值;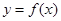 的图像上存在两点A,B使得
的图像上存在两点A,B使得 是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在
是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在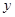 轴上,求实数
轴上,求实数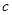 的取值范围;
的取值范围;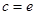 时,讨论关于
时,讨论关于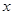 的方程
的方程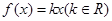 的实根个数.
的实根个数. +x(a≠0),
+x(a≠0),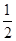 ,求证:当x∈(0,+∞)时,f(x)>1;
,求证:当x∈(0,+∞)时,f(x)>1; <e4(n∈N*)..
<e4(n∈N*)..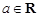 ,函数
,函数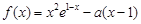 .
.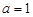 时,求
时,求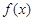 在
在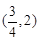 内的极大值;
内的极大值;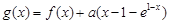 ,当
,当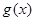 有两个极值点
有两个极值点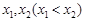 时,总有
时,总有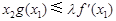 ,求实数
,求实数 的值.(其中
的值.(其中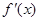 是
是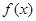 的导函数.)
的导函数.)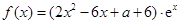 (
(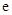 为自然对数的底数).
为自然对数的底数).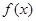 在
在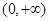 上的单调区间;
上的单调区间;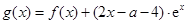 ,是否存在区间
,是否存在区间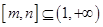 ,使得当
,使得当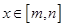 时函数
时函数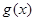 的值域为
的值域为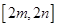 ,若存在求出
,若存在求出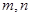 ,若不存在说明理由.
,若不存在说明理由.