题目内容
 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1,连接AP交棱CC1于点D.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1,连接AP交棱CC1于点D.
(Ⅰ)求证:PB1∥平面BDA1;
(Ⅱ)求二面角A-A1D-B的平面角的余弦值.
解:以A1为原点,A1B,A1C,A1A分别为x轴,y轴,z轴正方向,建立坐标系,
则A1(0,0,0),B1(1,0,0),C1(0,1,0),B(1,0,1),P(0,2,0)
(1)在△PAA1中,C1D= AA1,则D(0,1,
AA1,则D(0,1, )
)
∴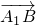 =(1,0,1),
=(1,0,1), =(0,1,
=(0,1, ),
), =(-1,2,0)
=(-1,2,0)
设平面BDA1的一个法向量为 =(a,b,c)
=(a,b,c)
则
令c=-1,则 =(1,
=(1, ,-1)
,-1)
∵ •
• =1×(-1)+
=1×(-1)+ ×2+(-1)×0=0
×2+(-1)×0=0
∴PB1∥平面BDA1
(II)由(I)知平面BDA1的一个法向量 =(1,
=(1, ,-1)
,-1)
又 =(1,0,0)为平面AA1D的一个法向量
=(1,0,0)为平面AA1D的一个法向量
∴cos< ,
, >=
>= =
= =
=
故二面角A-A1D-B的平面角的余弦值为
分析:以A1为原点,A1B,A1C,A1A分别为x轴,y轴,z轴正方向,建立坐标系,则我们易求出各个点的坐标,进而求出各线的方向向量及各面的法向量.
(I)要证明PB1∥平面BDA1,我们可以先求出直线PB1的向量,及平面BDA1的法向量,然后判断证明这两个向量互相垂直
(II)由图象可得二面角A-A1D-B是一个锐二面角,我们求出平面AA1D与平面A1DB的法向量,然后求出两个法向量夹角的余弦值,得到结论.
点评:利用向量法求空间夹角问题,包括以下几种情况:
空间两条直线夹角的余弦值等于他们方向向量夹角余弦值的绝对值;
空间直线与平面夹角的余弦值等于直线的方向向量与平面的法向量夹角的正弦值;
空间锐二面角的余弦值等于他的两个半平面方向向量夹角余弦值的绝对值;
则A1(0,0,0),B1(1,0,0),C1(0,1,0),B(1,0,1),P(0,2,0)
(1)在△PAA1中,C1D=
 AA1,则D(0,1,
AA1,则D(0,1, )
)∴
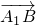 =(1,0,1),
=(1,0,1), =(0,1,
=(0,1, ),
), =(-1,2,0)
=(-1,2,0)设平面BDA1的一个法向量为
 =(a,b,c)
=(a,b,c)则

令c=-1,则
 =(1,
=(1, ,-1)
,-1)∵
 •
• =1×(-1)+
=1×(-1)+ ×2+(-1)×0=0
×2+(-1)×0=0∴PB1∥平面BDA1
(II)由(I)知平面BDA1的一个法向量
 =(1,
=(1, ,-1)
,-1)又
 =(1,0,0)为平面AA1D的一个法向量
=(1,0,0)为平面AA1D的一个法向量∴cos<
 ,
, >=
>= =
= =
=
故二面角A-A1D-B的平面角的余弦值为

分析:以A1为原点,A1B,A1C,A1A分别为x轴,y轴,z轴正方向,建立坐标系,则我们易求出各个点的坐标,进而求出各线的方向向量及各面的法向量.
(I)要证明PB1∥平面BDA1,我们可以先求出直线PB1的向量,及平面BDA1的法向量,然后判断证明这两个向量互相垂直
(II)由图象可得二面角A-A1D-B是一个锐二面角,我们求出平面AA1D与平面A1DB的法向量,然后求出两个法向量夹角的余弦值,得到结论.
点评:利用向量法求空间夹角问题,包括以下几种情况:
空间两条直线夹角的余弦值等于他们方向向量夹角余弦值的绝对值;
空间直线与平面夹角的余弦值等于直线的方向向量与平面的法向量夹角的正弦值;
空间锐二面角的余弦值等于他的两个半平面方向向量夹角余弦值的绝对值;

练习册系列答案
相关题目




