题目内容
5.在平面直角坐标系中,横坐标和纵坐标均为整数的点称为整点,对任意自然数n,连接原点O与点An(n,n+5),若用f(n)表示线段OAn上除端点外的整点个数,则f(1)+f(2)+…+f(2011)=1608.分析 因为线段OAn斜率k=$\frac{n+5}{n}$=1+$\frac{5}{n}$,所在直线方程为y=x+$\frac{5}{n}$x,所以n为5的倍数,才能找出比n小的整数x,使得y也为整数.由此入手能够求出f(1)+f(2)+…+f(2011)的值.
解答 解:∵线段OAn斜率k=$\frac{n+5}{n}$=1+$\frac{5}{n}$,
所在直线方程为y=x+$\frac{5}{n}$x,
∴n为5的倍数,才能找出比n小的整数x,使得y也为整数.
∴当n=5,10,15,20,…,2010时,线段OAn上有除端点外的4个整点.
数列5,10,15,20,…,2010是首项为5,公差为5的等差数列,其通项公式为am=5m.
由5m=2010知m=402,
∴f(1)+f(2)+…+f(2010)=4×402=1608,
故答案为:1608
点评 本题考查数列的性质和应用,解题时要认真审题,挖掘题设条件中的隐含条件.

练习册系列答案
相关题目
13.下列推理所得结论正确的是( )
| A. | 由a(b+c)=ab+ac类比得到loga(x+y)=logax+logby | |
| B. | 由a(b+c)=ab+ac类比得到cos(x+y)=cosx+cosy | |
| C. | 由(a+b)c=ac+bc类比$\frac{a+b}{c}$=$\frac{a}{c}$+$\frac{b}{c}$(c≠0) | |
| D. | 由(ab)n=anbn类比得到(x+y)n=xn+yn |
10.根据如下样本数据:
得到的回归方程为$\overrightarrow{y}$=$\overrightarrow{b}$x+$\overrightarrow{a}$,则( )
| x | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 10 | 9 | 7 | 6 | 4 | 3 |
| A. | $\overrightarrow{a}$>0,$\overrightarrow{b}$>0 | B. | $\overrightarrow{a}$>0,$\overrightarrow{b}$<0 | C. | $\overrightarrow{a}$<0,$\overrightarrow{b}$>0 | D. | $\overrightarrow{a}$<0,$\overrightarrow{b}$<0 |
17.设m、n为两条不重合的直线,α,β为两个不重合的平面,下列命题中正确的是( )
| A. | 若m、n与α所成的角相等,则m∥n | B. | 若n∥α,m∥β,α∥β,则m∥n | ||
| C. | 若n?α,m?β,m∥n,则α∥β | D. | 若n⊥α,m⊥β,α⊥β,则n⊥m |
14.下列结论正确的是( )
| A. | 若ac>bc,则a>b | B. | 若a2>b2,则a>b | ||
| C. | 若a>b,c>d,则ac>bd | D. | 若a>b>0,则a>$\frac{a+b}{2}>\sqrt{ab}$>b |
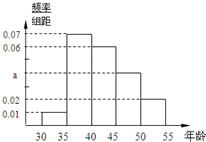 某同学对本地[30,55]岁的爱好阅读的人群随机抽取n人进行了一次调查,得到如下年龄统计表,其中不超过40岁的共有60人.
某同学对本地[30,55]岁的爱好阅读的人群随机抽取n人进行了一次调查,得到如下年龄统计表,其中不超过40岁的共有60人.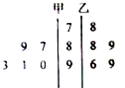 如图是甲、乙两位射击运动员的5次训练成绩(单位:环)的茎叶图,则成绩较为稳定(方差较小)的运动员是甲.
如图是甲、乙两位射击运动员的5次训练成绩(单位:环)的茎叶图,则成绩较为稳定(方差较小)的运动员是甲.