题目内容
某车间为了规定工时额,需确定加工零件所花费的时间,为此做了4次试验,得到的数据如下图:若加工时间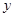 与零件个数
与零件个数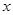 之间有较好的线性相关关系。(
之间有较好的线性相关关系。(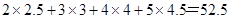 )
)
|
|
2 |
3 |
4 |
5 |
|
|
2.5 |
3 |
4 |
4.5 |
(1)求加工时间与零件个数的线性回归方程;
(2)试预报加工10个零件需要的时间。
(附:回归方程系数公式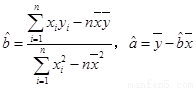 )
)
【答案】
(1) (2)约需要8.05小时
(2)约需要8.05小时
【解析】
试题分析:(1)根据表中数据可以求出 ,
,
根据公式可以求出 ,
,
再代入公式 ,可以求得
,可以求得
所以回归直线方程为 ;
10分
;
10分
(2)将x=10代入求出的回归直线中,可以解得
所以加工10个零件约需要8.05小时。 13分
考点:本小题主要考查回归直线方程的求解和应用.
点评:当变量之间具有线性相关关系时,求出的回归直线才有意义,另外,由回归直线得到的是估计值,而不是精确值.

练习册系列答案
相关题目
某车间为了规定工时额,需确定加工零件所花费的时间,为此做了4次试验,得到的数据如图:若加工时间y与零件个数x之间有较好的线性相关关系.(2×2.5+3×3+4×4+5×4.5=52.5)
(1)求加工时间与零件个数的线性回归方程;
(2)试预报加工10个零件需要的时间.
(附:回归方程系数公式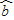 =
=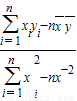 ,
,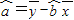 )
)
| x | 2 | 3 | 4 | 5 |
| y | 2.5 | 3 | 4 | 4.5 |
(2)试预报加工10个零件需要的时间.
(附:回归方程系数公式
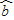 =
=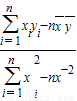 ,
,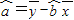 )
)


