题目内容
已知向量 且a1=1,若数列{an}的前n项和为Sn,且
且a1=1,若数列{an}的前n项和为Sn,且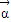 =λ
=λ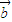 (λ∈R,λ≠0),则
(λ∈R,λ≠0),则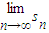 = .
= .
【答案】分析:由题意 =λ
=λ 成立,可得
成立,可得  ,由此知此数列为一公比为
,由此知此数列为一公比为  的等比数列,数列{an}的首项a1=1,求出其前n项之和为Sn,求其极限即可.
的等比数列,数列{an}的首项a1=1,求出其前n项之和为Sn,求其极限即可.
解答:解:由题意 =λ
=λ 成立,可得
成立,可得  ,
,
由此知此数列为一公比为 的等比数列,数列{an}的首项a1=1,
的等比数列,数列{an}的首项a1=1,
∴Sn= =
= =
=
∴ =
= =
=
故答案为: .
.
点评:本题考查数列的极限,解题的关键是根据向量的内积公式,得出数列的性质首项为1,公比为 的等比数列,求出其前n项之和为Sn,极限的运算法则也很关键.
的等比数列,求出其前n项之和为Sn,极限的运算法则也很关键.
 =λ
=λ 成立,可得
成立,可得  ,由此知此数列为一公比为
,由此知此数列为一公比为  的等比数列,数列{an}的首项a1=1,求出其前n项之和为Sn,求其极限即可.
的等比数列,数列{an}的首项a1=1,求出其前n项之和为Sn,求其极限即可.解答:解:由题意
 =λ
=λ 成立,可得
成立,可得  ,
,由此知此数列为一公比为
 的等比数列,数列{an}的首项a1=1,
的等比数列,数列{an}的首项a1=1,∴Sn=
 =
= =
=
∴
 =
= =
=
故答案为:
 .
.点评:本题考查数列的极限,解题的关键是根据向量的内积公式,得出数列的性质首项为1,公比为
 的等比数列,求出其前n项之和为Sn,极限的运算法则也很关键.
的等比数列,求出其前n项之和为Sn,极限的运算法则也很关键. 
练习册系列答案
相关题目
 =(an+1,1),
=(an+1,1), =(an+1,1),n∈N+,且a1=2,
=(an+1,1),n∈N+,且a1=2,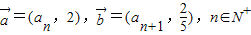 且a1=1,若数列{an}的前n项和为Sn,且
且a1=1,若数列{an}的前n项和为Sn,且 ,则
,则 =( )
=( )



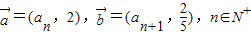 且a1=1,若数列{an}的前n项和为Sn,且
且a1=1,若数列{an}的前n项和为Sn,且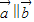 ,则
,则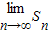 =( )
=( )



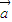 =(an+1,1),
=(an+1,1),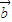 =(an+1,1),n∈N+,且a1=2,
=(an+1,1),n∈N+,且a1=2,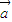 ∥
∥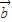 ,则数列{an}的前5项和为( )
,则数列{an}的前5项和为( )