题目内容
△ABC中，若(
+
)•
=
|
|2，则
的值为（ ）
| CA |
| CB |
| AB |
| 3 |
| 5 |
| AB |
| tanA |
| tanB |
| A．2 | B．4 | C．
| D．2
|
△ABC中，∵(
+
)•
=
|
|2，即
•
+
•
=
2，
∴bc•cos（π-A）+ac•cosB=
c2，
∴a•cosB-b•cosA=
c，
∴a•
-b•
=
c，即 a2-b2=
c2．
∴
=
=
=
=
=4，
故选B．
| CA |
| CB |
| AB |
| 3 |
| 5 |
| AB |
| CA |
| AB |
| CB |
| AB |
| 3 |
| 5 |
| AB |
∴bc•cos（π-A）+ac•cosB=
| 3 |
| 5 |
∴a•cosB-b•cosA=
| 3 |
| 5 |
∴a•
| a2+c 2-b2 |
| 2ac |
| b2+c 2-a2 |
| 2bc |
| 3 |
| 5 |
| 3 |
| 5 |
∴
| tanA |
| tanB |
| sinA•cosB |
| sinBcosA |
a•
| ||
b•
|
| a2-b2+c2 |
| b2-a2+c2 |
| ||
-
|
故选B．
练习册系列答案
相关题目
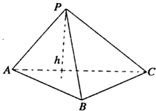在Rt△ABC中，CA⊥CB，斜边AB上的高为h1，则
，则
；类比此性质，在四面体P—ABC中，若
，底面ABC上的高为h，则
．