题目内容
 根据条件,分别求出椭圆的方程:
根据条件,分别求出椭圆的方程:(1)中心在原点,对称轴为坐标轴,离心率为
| 1 |
| 2 |
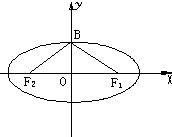
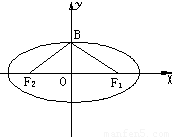
(2)中心在原点,对称轴为坐标轴,焦点在x轴上,短轴的一个顶点B与两个焦点F1,F2组成的三角形的周长为4+2
| 3 |
| 2π |
| 3 |
分析:(1)先求出椭圆中的长半轴长和短半轴长,再判断焦点位置,因为焦点位置不确定,所以求出的椭圆方程有两种形式.
(2)结合函数图形,通过直角三角形△F2OB推出a,c的关系,利用周长得到第二个关系,求出a,c然后求出b,求出椭圆的方程.
(2)结合函数图形,通过直角三角形△F2OB推出a,c的关系,利用周长得到第二个关系,求出a,c然后求出b,求出椭圆的方程.
解答:解:(1)∵椭圆的长轴长为8,即2a=8,
∴a=4,∵离心率为
,即e=
=
,∴c=2
∵b2=a2-c2,∴b2=16-4=12,
当椭圆焦点在x轴上时,椭圆方程为
+
=1
当椭圆焦点在y轴上时,椭圆方程为
+
=1.
所求椭圆方程为:
+
=1或
+
=1
(2)设长轴为2a,焦距为2c,则在△F2OB中,由∠F2BO=
得:c=
a,
所以△F2OF1的周长为:2a+2c=4+2
,∴a=2,c=
,∴b2=1
故得:
+y2=1.
∴a=4,∵离心率为
| 1 |
| 2 |
| c |
| a |
| 1 |
| 2 |
∵b2=a2-c2,∴b2=16-4=12,
当椭圆焦点在x轴上时,椭圆方程为
| x2 |
| 16 |
| y2 |
| 12 |
当椭圆焦点在y轴上时,椭圆方程为
| y2 |
| 16 |
| x2 |
| 12 |
所求椭圆方程为:
| x2 |
| 16 |
| y2 |
| 12 |
| y2 |
| 16 |
| x2 |
| 12 |
(2)设长轴为2a,焦距为2c,则在△F2OB中,由∠F2BO=
| π |
| 3 |
| ||
| 2 |
所以△F2OF1的周长为:2a+2c=4+2
| 3 |
| 3 |
故得:
| x2 |
| 4 |
点评:本题主要考查考察查了椭圆的标准方程的求法,关键是求出a,b的值,易错点是没有判断焦点位置.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
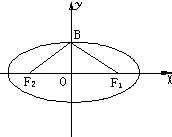 根据条件,分别求出椭圆的方程:
根据条件,分别求出椭圆的方程: ,长轴长为8;
,长轴长为8; ,且
,且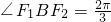 .
. ,长轴长为8;
,长轴长为8;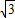 ,且
,且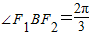 .
.
 ,长轴长为8;
,长轴长为8;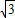 ,且
,且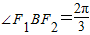 .
.