题目内容
设椭圆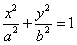 (a>b>0)的左焦点为F1(-2,0),左准线
(a>b>0)的左焦点为F1(-2,0),左准线 与x轴交于点N(-3,0),过点N倾斜角为30°的直线
与x轴交于点N(-3,0),过点N倾斜角为30°的直线 交椭圆于A,B两点。
交椭圆于A,B两点。
(1)求直线 和椭圆的方程;
和椭圆的方程;
(2)求证:点F1(-2,0)在以线段AB为直径的圆上。
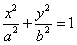 (a>b>0)的左焦点为F1(-2,0),左准线
(a>b>0)的左焦点为F1(-2,0),左准线 与x轴交于点N(-3,0),过点N倾斜角为30°的直线
与x轴交于点N(-3,0),过点N倾斜角为30°的直线 交椭圆于A,B两点。
交椭圆于A,B两点。(1)求直线
 和椭圆的方程;
和椭圆的方程;(2)求证:点F1(-2,0)在以线段AB为直径的圆上。
解:(1)由题意,知椭圆的焦点在x轴上,
且 ,∴a2=6,b2=2,
,∴a2=6,b2=2,
∴椭圆的方程为 ,
,
直线 的方程为
的方程为 。
。
(2)设A ,B
,B ,
,
由题意,直线 的方程为
的方程为 ,
,
将直线 代入椭圆
代入椭圆 ,
,
有 ,
,
∵ ,
, ,
,
 ,
,
又∵ ,
, ,
,
∴
 ,
,
∴ ,
,
∴点 在以线段为直径的圆上。
在以线段为直径的圆上。
且
 ,∴a2=6,b2=2,
,∴a2=6,b2=2,∴椭圆的方程为
 ,
,直线
 的方程为
的方程为 。
。(2)设A
 ,B
,B ,
,由题意,直线
 的方程为
的方程为 ,
,将直线
 代入椭圆
代入椭圆 ,
,有
 ,
,∵
 ,
, ,
, ,
,又∵
 ,
, ,
,∴

 ,
,∴
 ,
,∴点
 在以线段为直径的圆上。
在以线段为直径的圆上。
练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目












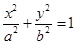 (a>b>0)的两焦点为F1、F2,若椭圆上存在一点Q,使∠F1QF2=120º,椭圆离心率e的取值范围为( )
(a>b>0)的两焦点为F1、F2,若椭圆上存在一点Q,使∠F1QF2=120º,椭圆离心率e的取值范围为( )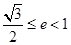 B.
B.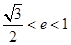 C.
C.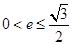 D.
D.
 (“a>b〉0)的左焦点为
(“a>b〉0)的左焦点为 ,椭圆过点P(
,椭圆过点P( )
) 与椭圆C交于A、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围.
与椭圆C交于A、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围.