题目内容
两等差数列{an}和{bn},前n项和分别为Sn,Tn,且
=
,则
=
.
| Sn |
| Tn |
| 7n+2 |
| n+3 |
| a2+a20 |
| b7+b15 |
| 149 |
| 24 |
| 149 |
| 24 |
分析:在{an}为等差数列中,当m+n=p+q(m,n,p,q∈N+)时,am+an=ap+aq.所以结合此性质可得:
=
=
,再根据题意得到答案.
| a2+a20 |
| b7+b15 |
21×(a1+a21)×
| ||
21×(b1+b21)×
|
| S21 |
| T21 |
解答:解:在{an}为等差数列中,当m+n=p+q(m,n,p,q∈N+)时,am+an=ap+aq.
所以
=
=
,
又因为
=
,
所以
=
.
故答案为:
.
所以
| a2+a20 |
| b7+b15 |
21×(a1+a21)×
| ||
21×(b1+b21)×
|
| S21 |
| T21 |
又因为
| Sn |
| Tn |
| 7n+2 |
| n+3 |
所以
| a2+a20 |
| b7+b15 |
| 149 |
| 24 |
故答案为:
| 149 |
| 24 |
点评:本题主要考查等差数列的性质,即在{an}为等差数列中,当m+n=p+q(m,n,p,q∈N+)时,am+an=ap+aq,此题属于基础题型.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 ,则
,则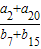 = .
= .