题目内容
下列平面图形中与空间的平行六面体作为类比对象较合适的是( )
| A.三角形 | B.梯形 | C.平行四边形 | D.矩形 |
C
解析试题分析:根据题意 ,由于平面图形中与空间的平行六面体作为类比对象,那么最适合的为平行四边形的运用,故可知答案为C.
考点:类比推理
点评:主要是考查了类比推理的运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下面四个判断中,正确的是( )
| A.式子1+k+k2+…+kn(n∈N*)中,当n=1时式子值为1 |
| B.式子1+k+k2+…+kn-1(n∈N*)中,当n=1时式子值为1+k |
C.式子1+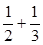 +…+ +…+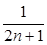 (n∈N*)中,当n=1时式子值为1+ (n∈N*)中,当n=1时式子值为1+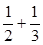 |
D.设f(x)=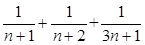 (n∈N*),则f(k+1)=f(k)+ (n∈N*),则f(k+1)=f(k)+ |
设 是定义在正整数集上的函数,且
是定义在正整数集上的函数,且 满足:“当
满足:“当 成立时,总可推出
成立时,总可推出 成立”,那么,下列命题总成立的是 ( )
成立”,那么,下列命题总成立的是 ( )
A.若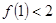 成立,则 成立,则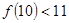 成立 成立 |
B.若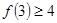 成立,则当 成立,则当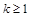 时,均有 时,均有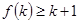 成立 成立 |
C.若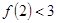 成立,则 成立,则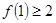 成立 成立 |
D.若 成立,则当 成立,则当 时,均有 时,均有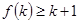 成立 成立 |
用反证法证明命题“如果你 ,那么
,那么 ”时,假设的内容是
”时,假设的内容是
A.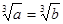 | B. |
C.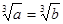 且 且 | D.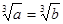 或 或 |
有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线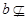 平面
平面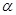 ,直线
,直线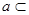 平面
平面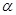 ,直线
,直线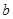 ∥平面
∥平面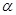 ,则直线
,则直线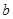 ∥直线
∥直线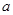 ”的结论显然是错误的,这是因为 ( )
”的结论显然是错误的,这是因为 ( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |
用数学归纳法证明等式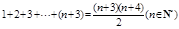 时,第一步验证
时,第一步验证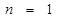 时,左边应取的项是
时,左边应取的项是
| A.1 | B.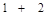 | C. | D.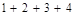 |
由“半径为R的圆内接矩形中,正方形的面积最大”,推理出“半径为R的球的内接长方体中,正方体的体积最大”是( )
| A.归纳推理 | B.类比推理 | C.演绎推理 | D.以上都不是 |
下列代数式(其中k∈N*)能被9整除的是( )
| A.6+6·7k | B.2+7k-1 |
| C.2(2+7k+1) | D.3(2+7k) |
 ,…,根据上述规律,第五个等式为______________.
,…,根据上述规律,第五个等式为______________.