题目内容
设等比数列{an}的前n项和为Sn,且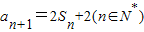 .
.(1)求数列{an}的通项公式;
(2)在an与an+1之间插入n个数,使这n+2个数成公差为dn的等差数列(如在a1与a2之间插入1个数构成第1个等差数列,其公差为d1;在a2与a3之间插入2个数构成第2个等差数列,其公差为d2,…,以此类推),设第n个等差数列的和是An,
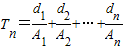 ,求Tn.
,求Tn.
【答案】分析:(1)an+1=2Sn+2可得an=2Sn-1+2(n≥2),两式相减可得an+1-an=2an然后由等比数列的定义可得;
(2)由公差的定义可得An,进而可得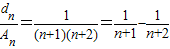 ,下面用裂项相消法求解即可.
,下面用裂项相消法求解即可.
解答:解:(1)∵an+1=2Sn+2
∴an=2Sn-1+2(n≥2)…(1分)
两式相减可得an+1-an=2an…(2分)
∴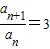 …(3分)
…(3分)
在an+1=2Sn+2中令n=1,得a1=2…(5分)
由等比数列的通项公式可得: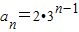 …(6分)
…(6分)
(2)证明: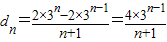 …(7分)
…(7分)
An=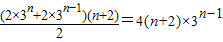 …(8分)
…(8分)
∴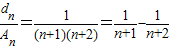 …(10分)
…(10分)
∴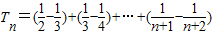 …(11分)
…(11分)
=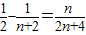 …(12分)
…(12分)
点评:本题为数列的通项公式和求和的综合题目,涉及等比数列的定义和裂项相消法求和,属中档题.
(2)由公差的定义可得An,进而可得
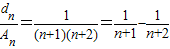 ,下面用裂项相消法求解即可.
,下面用裂项相消法求解即可.解答:解:(1)∵an+1=2Sn+2
∴an=2Sn-1+2(n≥2)…(1分)
两式相减可得an+1-an=2an…(2分)
∴
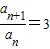 …(3分)
…(3分)在an+1=2Sn+2中令n=1,得a1=2…(5分)
由等比数列的通项公式可得:
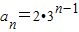 …(6分)
…(6分)(2)证明:
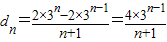 …(7分)
…(7分)An=
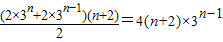 …(8分)
…(8分)∴
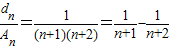 …(10分)
…(10分)∴
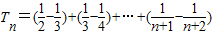 …(11分)
…(11分)=
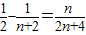 …(12分)
…(12分)点评:本题为数列的通项公式和求和的综合题目,涉及等比数列的定义和裂项相消法求和,属中档题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
设等比数列{an}的前n项和为Sn,若8a2+a5=0,则下列式子中数值不能确定的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设等比数列{an}的前n项和为Sn,若
=3,则
=( )
| S6 |
| S3 |
| S9 |
| S6 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |