题目内容
设![]() ,
,![]() 是两个非零向量,下列说法正确的是( )
是两个非零向量,下列说法正确的是( )
|
| A. | 若 | B. | 若 |
|
| C. | 若 | D. | 若存在实数λ,使得 |
考点:
数量积判断两个平面向量的垂直关系.
专题:
平面向量及应用.
分析:
根据选择项知需要判断命题的真假,由数量积运算将![]() 两边平方后化简说明C正确、A错、B错,再对
两边平方后化简说明C正确、A错、B错,再对![]() 两边取模后,代入
两边取模后,代入![]() 进行验证D错.
进行验证D错.
解答:
解:设非零向量![]() ,
,![]() 的夹角是θ,
的夹角是θ,
①将![]() 两边平方得,
两边平方得,![]() ,
,
即![]() ,得cosθ=﹣1,
,得cosθ=﹣1,
则![]() ,
,![]() 是共线向量,即存在实数λ,
是共线向量,即存在实数λ,![]() ,则C正确,A错;
,则C正确,A错;
另:当![]() 时,有
时,有![]() ,代入
,代入![]() ,显然不成立,故B错;
,显然不成立,故B错;
②存在实数λ,![]() 时,
时,
则![]() ,
,![]() ,
,
故![]() 不一定成立,故D错.
不一定成立,故D错.
故选C.
点评:
本题考查了向量的平方就是向量模的平方应用,以及数量积的运算,考查了分析问题和解决问题的能力.

练习册系列答案
相关题目
设![]() ,
,![]() 是两个非零向量( )
是两个非零向量( )
|
| A. | 若| | B. | 若 |
|
| C. | 若| | D. | 若存在实数λ,使得 |
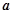 ,
,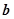 是两个非零向量( )
是两个非零向量( )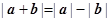 ,则
,则
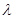 ,使得
,使得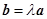
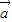 ,
,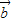 是两个非零向量,下列说法正确的是( )
是两个非零向量,下列说法正确的是( ) =
=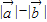 ,则
,则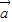 ⊥
⊥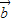
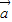 ⊥
⊥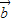 ,则
,则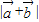 =
=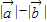
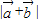 =
=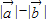 ,则存在实数λ,使得
,则存在实数λ,使得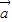 =λ
=λ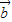
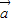 =λ
=λ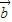 ,则
,则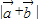 =
=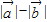
 ,
, 是两个非零向量( )
是两个非零向量( ) +
+ |=|
|=| |-|
|-| |,则
|,则 ⊥
⊥
 ⊥
⊥ ,则|
,则| +
+ |=|
|=| |-|
|-| |
| +
+ |=|
|=| |-|
|-| |,则存在实数λ,使得
|,则存在实数λ,使得 =λ
=λ
 =λ
=λ ,则|
,则| +
+ |=|
|=| |-|
|-| |
|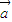 ,
,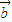 是两个非零向量,则“向量
是两个非零向量,则“向量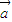 ,
,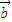 的夹角为锐角”是“函数f(x)=(x
的夹角为锐角”是“函数f(x)=(x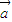 +
+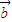 )•(
)•(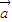 -x
-x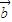 )的图象是一条开口向下的抛物线”的( )
)的图象是一条开口向下的抛物线”的( )