题目内容
已知△ABC的三个顶点均在球O的球面上，且AB=AC=1，∠BAC=120°，直线OA与平面ABC所成的角的正弦值为
，则球面上B、C两点间的球面距离为______．
| ||
| 3 |
在三角形ABC中，AB=AC=1，∠BAC=120°，
∴由余弦定理得BC=
| 3 |
由正弦定理得，三角形ABC外接圆的半径O′B=
| 3 |
又直线OA与平面ABC所成的角的正弦值为
| ||
| 3 |
∴
| AO′ |
| OA |
| 3 |
在三角形BCO′中，
∠BO′C=
| π |
| 3 |
| 3 |
则球面上B、C两点间的球面距离为：
| π |
| 3 |
| 3 |
| ||
| 3 |
故答案为：
| ||
| 3 |
练习册系列答案
阅读快车系列答案
相关题目
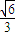，则球面上B、C两点间的球面距离为 ．