题目内容
是否存在中心在坐标原点,长轴在x轴上的椭圆,使它的离心率e=
,且点P(0,
)到这个椭圆上的点的最远距离为7?若存在,求出这个方程,并求椭圆上到点P的距离等于7的点的坐标;若不存在,请说明理由.
解:假设存在这样的椭圆.∵e==,
设所求椭圆方程为
=1,
∴x2=4b2-4y2.
设椭圆上的点(x,y)到点P的距离为d,
则d2=x2+(y-
)2=4b2-3y2-3y+
=-3(y+
)2+4b2+3,其中-b≤y≤b.
若b＜
,则当y=-b时,d2有最大值=4b2+3=(
)2.
解得b2=1与b＜
矛盾.
因此必有b≥
成立,于是当y=-
时,d2(从而d)有最大值.
∴(
)2=4b2+3,解得b=1,a=2.
故所求椭圆的标准方程为
+y2=1.
由y=-
及求得的椭圆方程可得,椭圆上的点(
,-
)、(-
,-
)到点P的距离都是
.
练习册系列答案
相关题目
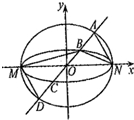（2013•湖北）如图，已知椭圆C1与C2的中心在坐标原点O，长轴均为MN且在x轴上，短轴长分别为2m，2n（m＞n），过原点且不与x轴重合的直线l与C1，C2的四个交点按纵坐标从大到小依次为A，B，C，D，记
（2011•延庆县一模）已知椭圆C的中心在坐标原点，焦点在x轴上，它的一个顶点B与抛物线x2=4y的焦点重合，离心率