题目内容
已知a,b,c均为正数,证明:a2+b2+c2+(| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 3 |
分析:证法一:两次利用基本不等式放小,此处不用考虑等号成立的条件,因等号不成立不影响不等号的传递性.
证法二:先用基本不等式推出a2+b2+c2≥ab+bc+ac与
+
+
≥
+
+
两者之和用基本不等式放小,整体上只用了一次放缩法.其本质与证法一同.
证法二:先用基本不等式推出a2+b2+c2≥ab+bc+ac与
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| c2 |
| 1 |
| ab |
| 1 |
| bc |
| 1 |
| ac |
解答:证明:
(证法一)
因为a,b,c均为正数,由平均值不等式得
①
所以(
+
+
)2≥9(abc)-
②(6分)
故a2+b2+c2+(
+
+
)2≥3(abc)
+9(abc)-
.
又3(abc)
+9(abc)-
≥2
=6
③
所以原不等式成立.(8分)
当且仅当a=b=c时,①式和②式等号成立.当且仅当3(abc)
=9(abc)-
时,③式等号成立.
即当且仅当a=b=c=3
时,原式等号成立.(10分)
(证法二)
因为a,b,c均为正数,由基本不等式得
所以a2+b2+c2≥ab+bc+ac①
同理
+
+
≥
+
+
②(6分)
故a2+b2+c2+(
+
+
)2③
≥ab+bc+ac+3
+3
+3
≥6
所以原不等式成立.(8分)
当且仅当a=b=c时,①式和②式等号成立,当且仅当a=b=c,(ab)2=(bc)2=(ac)2=3时,③式等号成立.
即当且仅当a=b=c=3
时,原式等号成立.(10分)
(证法一)
因为a,b,c均为正数,由平均值不等式得
|
所以(
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 2 |
| 3 |
故a2+b2+c2+(
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 2 |
| 3 |
| 2 |
| 3 |
又3(abc)
| 2 |
| 3 |
| 2 |
| 3 |
| 27 |
| 3 |
所以原不等式成立.(8分)
当且仅当a=b=c时,①式和②式等号成立.当且仅当3(abc)
| 2 |
| 3 |
| 2 |
| 3 |
即当且仅当a=b=c=3
| 1 |
| 4 |
(证法二)
因为a,b,c均为正数,由基本不等式得
|
所以a2+b2+c2≥ab+bc+ac①
同理
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| c2 |
| 1 |
| ab |
| 1 |
| bc |
| 1 |
| ac |
故a2+b2+c2+(
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
≥ab+bc+ac+3
| 1 |
| ab |
| 1 |
| bc |
| 1 |
| ac |
≥6
| 3 |
当且仅当a=b=c时,①式和②式等号成立,当且仅当a=b=c,(ab)2=(bc)2=(ac)2=3时,③式等号成立.
即当且仅当a=b=c=3
| 1 |
| 4 |
点评:考查放缩法在证明不等式中的应用,本题在用缩法时多次用到基本不等式,请读者体会本题证明过程中不考虑等号是否成立的原理,并与利用基本不等式求最值再据最值成立的条件求参数题型比较.深入分析等号成立的条件什么时候必须考虑,什么时候可以不考虑.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
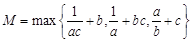 ,则M的最小值为 .
,则M的最小值为 .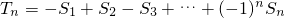 ,求满足不等式
,求满足不等式 的所有n的值;
的所有n的值;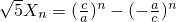 (n∈N+),证明:数列{
(n∈N+),证明:数列{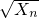 }中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.
}中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.