题目内容
已知函数f（x）=x|x-2|，x∈R．
（1）求不等式-3＜f（x）＜3的解集；
（2）设f（x）在[0，a]上的最大值为g（a），若
，求正实数a的取值范围．
解：（1）由题意不等式-3＜f（x）＜3，化为不等式-3＜x|x-2|＜3，
当x＜2时，不等式为：-3＜2x-x2＜3，即
，
解得-1＜x＜2；
当x≥2时，不等式-3＜x|x-2|＜3为：-3＜x2-2x＜3，即
，
解得：2≤x＜3；
综上不等式的解集为：{x|-1＜x＜3}．
（2）函数f（x）=x|x-2|=
，
函数f（x）在[0，a]上的最大值为g（a）=
，
由，可得：0＜a≤2时，2a-a2＜a
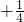，解得：0＜a≤2且a
；
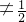1＜a≤1+
时，1＜a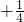，解得：1＜a≤1+，
a≥1+时，a2-2a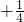＜a，解得a＞
；
综上a的取值范围是：{a|
或1＜a≤1+或a＞}
分析：（1）通过分类讨论直接求解不等式的解集即可．
（2）求出函数在[0，a]上的最大值为g（a）的表达式，利用得到不等式求解即可．
点评：本题考查绝对值不等式的解法，函数与分的综合应用，函数的最大值的求法，考查分类讨论思想的应用．
当x＜2时，不等式为：-3＜2x-x2＜3，即
，解得-1＜x＜2；
当x≥2时，不等式-3＜x|x-2|＜3为：-3＜x2-2x＜3，即
，解得：2≤x＜3；
综上不等式的解集为：{x|-1＜x＜3}．
（2）函数f（x）=x|x-2|=
，函数f（x）在[0，a]上的最大值为g（a）=
，由
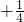，可得：0＜a≤2时，2a-a2＜a，解得：0＜a≤2且a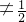；1＜a≤1+
时，1＜a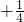，解得：1＜a≤1+，a≥1+
时，a2-2a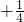＜a，解得a＞；综上a的取值范围是：{a|
或1＜a≤1+或a＞}分析：（1）通过分类讨论直接求解不等式的解集即可．
（2）求出函数在[0，a]上的最大值为g（a）的表达式，利用
得到不等式求解即可．点评：本题考查绝对值不等式的解法，函数与分的综合应用，函数的最大值的求法，考查分类讨论思想的应用．
练习册系列答案
互动英语系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|