题目内容
焦点在x轴上的椭圆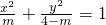
的离心率为
，则m的值为________．
3
分析：先根据椭圆焦点位置，确定椭圆的特征量a、b、c的表达式，再利用离心率定义列方程即可解得m的值
解答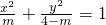：∵是焦点在x轴上的椭圆，
∴a2=m，b2=4-m，c2=2m-4
∵椭圆离心率为
=，
∴
=
=
解得m=3
故答案为 3
点评：本题考查了椭圆的标准方程及其几何性质，离心率的定义．
分析：先根据椭圆焦点位置，确定椭圆的特征量a、b、c的表达式，再利用离心率定义列方程即可解得m的值
解答：∵
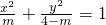是焦点在x轴上的椭圆，∴a2=m，b2=4-m，c2=2m-4
∵椭圆离心率为
=，∴
==解得m=3
故答案为 3
点评：本题考查了椭圆的标准方程及其几何性质，离心率的定义．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
，与直线x+y－1=0相交于两点Ｍ、Ｎ，且以
为直径的圆经过坐标原点．求椭圆的方程．
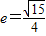，左顶点A（-4，0），圆O'：（x-2）2+y2=r2是椭圆G的内接△ABC的内切圆．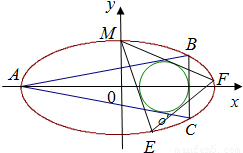
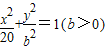经过点M（4，1），直线l：y=x+m交椭圆于A，B两不同的点．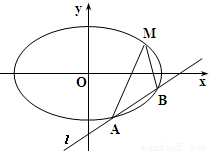
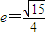，左顶点A（-4，0），圆O'：（x-2）2+y2=r2是椭圆G的内接△ABC的内切圆．