题目内容
以半径为1的圆内任一点为中点作弦，则弦长超过圆内接等边三角形边长的概率是（ ）
分析：由题意可得：符合条件的点必须在内接等边三角形的内切圆内，所求概率为两圆的面积比，由几何知识易得．
解答：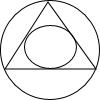
解：由题意可得：符合条件的点必须在内接等边三角形的内切圆内，
理由如下：因为两圆的圆心相同，大圆的半径为1，故内接正三角形的边长为
故内接等边三角形的内切圆半径为
故=
=
=
故选C
解：由题意可得：符合条件的点必须在内接等边三角形的内切圆内，理由如下：因为两圆的圆心相同，大圆的半径为1，故内接正三角形的边长为
| 3 |
故内接等边三角形的内切圆半径为
| 1 |
| 2 |
故=
| S小圆 |
| S大圆 |
π(
| ||
| π12 |
| 1 |
| 4 |
故选C
点评：本题为几何概型的求解，找到各自的度量是解决问题的关键，属中档题．
练习册系列答案
相关题目
（2013•湖南）在平面直角坐标系xOy中，将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“L路径”．如图所示的路径MM1M2M3N与路径MN1N都是M到N的“L路径”．某地有三个新建居民区，分别位于平面xOy内三点A（3，20），B（-10，0），C（14，0）处．现计划在x轴上方区域（包含x轴）内的某一点P处修建一个文化中心．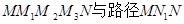
都是M到N的“L路径”。某地有三个新建的居民区，分别位于平面xOy内三点
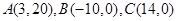处。现计划在x轴上方区域（包含x轴）内的某一点P处修建一个文化中心。
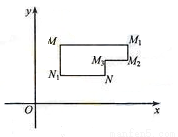
在平面直角坐标系xOy中，将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“L路径”．如图所示的路径MM1M2M3N与路径MN1N都是M到N的“L路径”．某地有三个新建居民区，分别位于平面xOy内三点A（3，20），B（-10，0），C（14，0）处．现计划在x轴上方区域（包含x轴）内的某一点P处修建一个文化中心．
在平面直角坐标系xOy中，将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“L路径”．如图所示的路径MM1M2M3N与路径MN1N都是M到N的“L路径”．某地有三个新建居民区，分别位于平面xOy内三点A（3，20），B（-10，0），C（14，0）处．现计划在x轴上方区域（包含x轴）内的某一点P处修建一个文化中心．