题目内容
(本小题满分12分)
甲打靶射击,有4发子弹,其中有一发是空弹(“空弹”即只有弹体没有弹头的子弹).
(1)如果甲只射击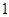 次,求在这一枪出现空弹的概率;
次,求在这一枪出现空弹的概率;
(2)如果甲共射击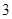 次,求在这三枪中出现空弹的概率;
次,求在这三枪中出现空弹的概率;
(3)如果在靶上画一个边长为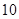 的等边
的等边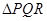 ,甲射手用实弹瞄准了三角形
,甲射手用实弹瞄准了三角形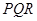 区域随机射击,且弹孔都落在三角形
区域随机射击,且弹孔都落在三角形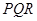 内。求弹孔与
内。求弹孔与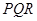 三个顶点的距离都大于1的概率(忽略弹孔大小).
三个顶点的距离都大于1的概率(忽略弹孔大小).
甲打靶射击,有4发子弹,其中有一发是空弹(“空弹”即只有弹体没有弹头的子弹).
(1)如果甲只射击
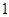 次,求在这一枪出现空弹的概率;
次,求在这一枪出现空弹的概率;(2)如果甲共射击
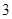 次,求在这三枪中出现空弹的概率;
次,求在这三枪中出现空弹的概率; (3)如果在靶上画一个边长为
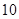 的等边
的等边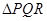 ,甲射手用实弹瞄准了三角形
,甲射手用实弹瞄准了三角形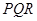 区域随机射击,且弹孔都落在三角形
区域随机射击,且弹孔都落在三角形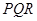 内。求弹孔与
内。求弹孔与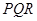 三个顶点的距离都大于1的概率(忽略弹孔大小).
三个顶点的距离都大于1的概率(忽略弹孔大小).(1) 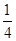 (2)
(2)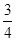 (3)
(3)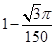
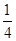 (2)
(2)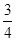 (3)
(3)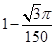
试题分析:设四发子弹编号为0(空弹),1,2,3。
(1)甲只射击
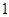 次,共有4个基本事件。
次,共有4个基本事件。设第一枪出现“哑弹”的事件为A,则
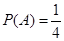 .
. (2)甲共射击
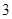 次,前三枪共有4个基本事件:{0,1,2},{0,1,3},{0,2,3},{1,2,3};
次,前三枪共有4个基本事件:{0,1,2},{0,1,3},{0,2,3},{1,2,3};设“甲共射击
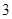 次,这三枪中出现空弹”的事件为B,
次,这三枪中出现空弹”的事件为B,B包含的的事件有三个:{0,1,2},{0,1,3},{0,2,3},
则
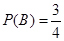 。
。 (3)等边
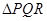 的面积为
的面积为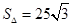 ,
, 分别以
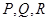 为圆心、1为半径的三个扇形的面积和为:
为圆心、1为半径的三个扇形的面积和为: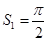 ,
, 设“弹孔与
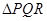 三个顶点的距离都大于1”的事件为C,
三个顶点的距离都大于1”的事件为C,则
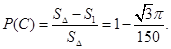
点评:本题考查古典概型、几何概型的计算,关键是理解、区分古典概型、几何概型两个不同的概念,并正确使用列举法求出基本事件的数目.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目




 贵州省高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出
贵州省高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出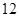 人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表: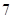 )班
)班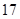 )班
)班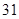 )班
)班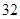 )班
)班 、
、 是常数,关于
是常数,关于 的一元二次方程
的一元二次方程 有实数解记为事件
有实数解记为事件 .
. ;
; 、
、 ,
, 且
且 ,求
,求 ,则
,则 的概率为
的概率为



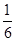
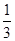
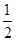
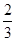
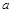 表示第1枚骰子出现的点数,
表示第1枚骰子出现的点数,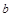 表示第2枚骰子出现的点数.
表示第2枚骰子出现的点数.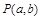 满足
满足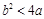 的概率;
的概率;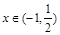 时,求函数
时,求函数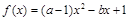 为单调函数的概率.
为单调函数的概率.