题目内容
已知中心为O的正方形ABCD的边长为2,点M、N分别为线段BC、CD上的两个不同点,且 ,则
,则 的取值范围是________.
的取值范围是________.

分析:由条件可得
 ≥
≥ ,求出
,求出 的最小值 和最大值,从而求得
的最小值 和最大值,从而求得 的最小值.当
的最小值.当 和
和  的模最大且夹角最小时,
的模最大且夹角最小时, 最大,故当M、N和点C重合时,
最大,故当M、N和点C重合时, 最大等于2,
最大等于2,再由点M、N分别为线段BC、CD上的两个不同点,可得
 的最大小于2,从而得到
的最大小于2,从而得到 的范围.
的范围.解答:由题意可得
 =
= =
= -2
-2 ≤1,
≤1,∴
 ≥
≥ .
.设CM=x,CN=y,则 MN2=x2+y2≤1.
 =1+(1-x)2+1+(1-y)2=(1-x)2+(1-y)2+2,
=1+(1-x)2+1+(1-y)2=(1-x)2+(1-y)2+2,表示单位圆面(x2+y2≤1 )上的点与点(1,1)连线的距离的平方加上2,
故其最小值为
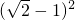 +2=5-2
+2=5-2 ,最大值为
,最大值为 +2=5+2
+2=5+2 .
.故
 的最小值等于
的最小值等于 =
= =2-
=2- .
.又当
 和
和  的模最大且夹角最小时,
的模最大且夹角最小时, 最大,
最大,故当M、N和点C重合时,
 最大等于
最大等于 •
• =2,
=2,再由点M、N分别为线段BC、CD上的两个不同点,可得
 的最大小于2.
的最大小于2.故
 的范围为[2-
的范围为[2- ,2).
,2).故答案为[2-
 ,2).
,2).点评:本题主要考查两个向量的加减法的法则,以及其几何意义,向量是数形结合的典型例子,向量的加减运算是用向量解决问题的基础,要学好运算,才能用向量解决立体几何问题,本题属于中档题.

练习册系列答案
相关题目
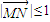 ,则
,则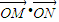 的取值范围是 .
的取值范围是 .