Question

已知函数f（x）=n（x-n+2m）（x-n-2m），g（x）=（

1

2

）^x-

1

4

，对?x∈R，有f（x）＞0或g（x）＞0．若m=n²-3n+a，则实数a的取值范围是

（-1，

41

16

）

．

Answer 1

分析：由g（x）＞0求出x的取值范围，利用补集思想得到f（x）＞0恒成立的x的范围，结合二次函数的零点的范围得到关于m和n的不等式组，画出可行域后结合函数m=n²-3n+a分析使a取得最值得可行域内的点，利用导数求出点的坐标后代入m=n²-3n+a即可求得a的最值，则答案可求．

解答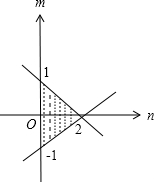：解：若g（x）＞0，即（

1

2

）^x-

1

4

＞0，则x＜2．
∵对?x∈R，有f（x）＞0或g（x）＞0，
∴当x≥2时，f（x）＞0恒成立．
又f（x）=n（x-n+2m）（x-n-2m），∴要使f（x）＞0对x≥2恒成立，
则有

n＞0 n-2m＜2 n+2m＜2

．以n为横轴，m为纵轴画出可行域如图，
∵m=n2-3n+a=(n-

3

2

)2+a-

9

4

是以直线n=

3

2

为对称轴，(

3

2

，a-

9

4

)为顶点，且开口向上的抛物线，
结合图形可知，当抛物线过点（0，-1）时，a取最小值-1；
当抛物线与直线n+2m-2=0相切时，a取最大值．
对函数m=n²-3n+a求导，得m′=2n-3．
∴2n-3=-

1

2

，解得n=

5

4

．将其代入n+2m-2=0，得m=

3

8

．
即切点坐标为(

5

4

，

3

8

)，此时a=

3

8

-(

5

4

)2+3×

5

4

=

41

16

为a的最大值．
∴实数a的取值范围是(-1，

41

16

)．
故答案为(-1，

41

16

)．

点评：本题考查了恒成立问题，考查了数学转化思想方法，训练了利用导数研究曲线上某点处的切线问题，是有一定难度的综合题目．