题目内容
数列an满足:log2an+1=1+log2an,前n项和为Sn,若a3=10,则a10=________.
330
分析:由log2an+1=1+log2an可得递推式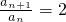 ,又a3=10,可求出
,又a3=10,可求出 ,根据求前n项和公式求出a10.
,根据求前n项和公式求出a10.
解答:由log2an+1=1+log2an,
log2an+1由log2an+1-log2an= =1,
=1,
可得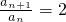 ,
,
又a3=a1+a2+a3=5a1=10,得 ,
,
因而a10=a1+…+a10= =330;
=330;
故答案为330.
点评:此题主要考查数列递推式及前n项和的计算.
分析:由log2an+1=1+log2an可得递推式
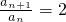 ,又a3=10,可求出
,又a3=10,可求出 ,根据求前n项和公式求出a10.
,根据求前n项和公式求出a10.解答:由log2an+1=1+log2an,
log2an+1由log2an+1-log2an=
 =1,
=1,可得
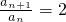 ,
,又a3=a1+a2+a3=5a1=10,得
 ,
,因而a10=a1+…+a10=
 =330;
=330;故答案为330.
点评:此题主要考查数列递推式及前n项和的计算.

练习册系列答案
相关题目