题目内容
点O在△ABC内部且满足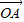 +2
+2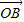 +2
+2 =
=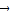 ,则△ABC的面积与△ABO的面积之比为 .
,则△ABC的面积与△ABO的面积之比为 .
【答案】分析:由已知向量等式,算出点O在△ABC的中线AD上,满足AO= AD,由此结合三角形的面积公式与三角形中线的性质,即可算出△ABC的面积与△ABO的面积之比.
AD,由此结合三角形的面积公式与三角形中线的性质,即可算出△ABC的面积与△ABO的面积之比.
解答:解: ∵
∵ +2
+2 +2
+2 =
= ,
,
∴
以OB、OC为邻边作平行四边形OBEC,
可得 =-
=-
 ,
,
因此,点O在△ABC的中线AD上,且满足AO= AD
AD
∴△ABO的面积S△ABO= S△ABD=
S△ABD= ×
× S△ABC=
S△ABC= S△ABC
S△ABC
可得△ABC的面积与△ABO的面积之比为 =
=
故答案为:
点评:本题给出向量等式,求两个三角形的面积之比.着重考查了平面向量的加法法则、三角形的面积公式等知识,属于中档题.
 AD,由此结合三角形的面积公式与三角形中线的性质,即可算出△ABC的面积与△ABO的面积之比.
AD,由此结合三角形的面积公式与三角形中线的性质,即可算出△ABC的面积与△ABO的面积之比.解答:解:
 ∵
∵ +2
+2 +2
+2 =
= ,
,∴

以OB、OC为邻边作平行四边形OBEC,
可得
 =-
=-
 ,
,因此,点O在△ABC的中线AD上,且满足AO=
 AD
AD∴△ABO的面积S△ABO=
 S△ABD=
S△ABD= ×
× S△ABC=
S△ABC= S△ABC
S△ABC可得△ABC的面积与△ABO的面积之比为
 =
=
故答案为:

点评:本题给出向量等式,求两个三角形的面积之比.着重考查了平面向量的加法法则、三角形的面积公式等知识,属于中档题.

练习册系列答案
相关题目