50=a0+a1x+a2x2+-+a50x50.其中a0•a1•a2-a50是常数.计算(a0+a2-+a50)-(a1+a3+a5+-+a49)=${}^{50}$．题目和参考答案——青夏教育精英家教网—

题目内容

3．（2-$\sqrt{3}$x）⁵⁰=a₀+a₁x+a₂x²+…+a₅₀x⁵⁰，其中a₀•a₁•a₂…a₅₀是常数，计算（a₀+a₂…+a₅₀）-（a₁+a₃+a₅+…+a₄₉）=${（2+\sqrt{3}）}^{50}$．

分析在所给的等式中，令x=-1，即可求得（a₀+a₂…+a₅₀）-（a₁+a₃+a₅+…+a₄₉）的值．

解答解：在（2-$\sqrt{3}$x）⁵⁰=a₀+a₁x+a₂x²+…+a₅₀x⁵⁰中，
令x=-1，可得（a₀+a₂…+a₅₀）-（a₁+a₃+a₅+…+a₄₉）=${（2+\sqrt{3}）}^{50}$，
故答案为：${（2+\sqrt{3}）}^{50}$．

点评本题主要考查二项式定理的应用，注意根据题意，分析所给代数式的特点，通过给二项式的x赋值，求展开式的系数和，可以简便的求出答案，属于基础题．

练习册系列答案

相关题目

16．在等比数列3，6，12，…中，第5项为（　　）

14．已知$M=\left\{{（x，y）\left|{y=\sqrt{1-{x^2}}}\right.}\right\}$，N={（x，y）|y=x+b}，若M∩N≠∅，则实数b的范围是（　　）

$[{-\sqrt{2}，\sqrt{2}}]$

11．已知$\sqrt{2+\frac{2}{3}}=2\sqrt{\frac{2}{3}}，\sqrt{3+\frac{3}{8}}=3\sqrt{\frac{3}{8}}，\sqrt{4+\frac{4}{15}}=4\sqrt{\frac{4}{15}}…$，若$\sqrt{6+\frac{a}{b}}=6\sqrt{\frac{a}{b}}$（a，b均为实数），请推测a=6，b=35．

18．已知等差数列{a_n}和{b_n}的前n项和分别为S_n，T_n，且$\frac{{S}_{n}}{{T}_{n}}$=$\frac{3n+1}{2n}$，则$\frac{a_5}{b_5}$=（　　）

8．当实数m为何值时，复数z=（m²-5m+6）+（m²-3m）i是：
（1）实数；
（2）纯虚数；
（3）复数z在一三象限平分线上．

15．

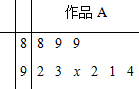我校开展“爱我河南，爱我方城”摄影比赛，9位评委为参赛作品A给出的分数如茎叶图所示，记分员在去掉一个最高分和一个最低分后，计算的平均分为91，复核员在复核时，发现一个数字（茎叶图中的x）无法看清，若记分员计算无误，则数字x应该是1．

12．函数y=$\frac{1}{2}$（e^x+e^-x）的导数是（　　）

A．

$\frac{1}{2}$（e ^x-e ^-x）

B．

$\frac{1}{2}$（e ^x+e ^-x）

13．（1）若cos（$\frac{π}{6}$+α）=$\frac{\sqrt{3}}{3}$，求tan（$\frac{5}{6}$π-α）的值．
（2）已知$\overrightarrow{a}$=（2，-1），$\overrightarrow{b}$=（-1，3），$\overrightarrow{c}$=（7，-11），x$\overrightarrow{a}$+y$\overrightarrow{b}$=$\overrightarrow{c}$，试求x，y的值．

试题分类