题目内容
已知等差数列 满足:
满足: ,
, 的前
的前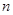 项和为
项和为 .
.
(1)求 及
及 ;
;
(2)令 (其中
(其中 为常数,且
为常数,且 ),求证数列
),求证数列 为等比数列.
为等比数列.
 满足:
满足: ,
, 的前
的前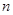 项和为
项和为 .
.(1)求
 及
及 ;
;(2)令
 (其中
(其中 为常数,且
为常数,且 ),求证数列
),求证数列 为等比数列.
为等比数列.(1) ;(2)详见解析.
;(2)详见解析.
 ;(2)详见解析.
;(2)详见解析.试题分析:(1)设出等差数列
 的公差为
的公差为 ,则由等差数列
,则由等差数列 的通项公式易将已知条件转化为
的通项公式易将已知条件转化为 和d的二元一次方程组,解此方程组可得到
和d的二元一次方程组,解此方程组可得到 和d的值,从而就可写出
和d的值,从而就可写出 及
及 ;(2)要证数列
;(2)要证数列 为等比数列,只需证
为等比数列,只需证 是常数对一切
是常数对一切 都成立即可,将已知与(1)的结论代入易知
都成立即可,将已知与(1)的结论代入易知 为常数,从而问题得证.
为常数,从而问题得证.试题解析:(1)设等差数列
 的公差为
的公差为 ,因为
,因为 ,所以有
,所以有 ,解得
,解得
所以

(2)由(1)知
 ,所以
,所以 .(
.( C是常数,
C是常数, 也是常数,且
也是常数,且 )所以数列
)所以数列 是以
是以 为首项,
为首项, 为公比的等比数列.
为公比的等比数列. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的前n项和为
的前n项和为 ,且
,且
 ,求数列
,求数列 的前n项和Tn.
的前n项和Tn.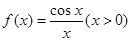 ,
,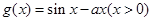 .
.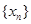 ,求
,求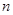 项和
项和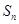 ;
; 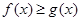 在
在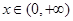 上恒成立,求实数
上恒成立,求实数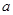 的取值范围;
的取值范围;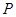 是函数
是函数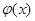 与
与 图象的交点,若直线
图象的交点,若直线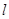 同时与函数
同时与函数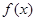 与
与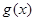 存在分切线?若存在,求出实数
存在分切线?若存在,求出实数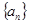 为等差数列,且
为等差数列,且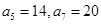 ,数列
,数列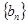 的前
的前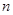 项和为
项和为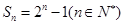 ,
,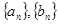 的通项公式;
的通项公式;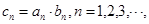 ,求数列
,求数列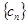 的前
的前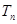 .
.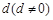 的等差数列,已知它的前10项和为
的等差数列,已知它的前10项和为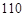 ,且a1,a2,a4 成等比数列.
,且a1,a2,a4 成等比数列.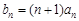 ,求数列
,求数列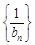 的前
的前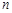 项和Tn .
项和Tn .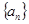 中,各项都是正数,且
中,各项都是正数,且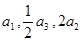 成等差数列,则
成等差数列,则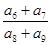 等于( )
等于( )



 ,且
,且 ,则
,则 的值为( )
的值为( )

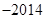
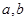 为正整数(
为正整数(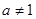 ),等差数列
),等差数列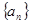 的首项为
的首项为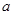 ,公差为
,公差为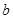 , 等比数列
, 等比数列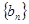 的首项为
的首项为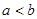 ,且
,且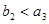 .在数列
.在数列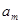 与
与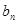 有
有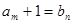 ,又设
,又设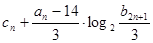 .
.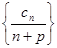 为等差数列,求常数
为等差数列,求常数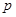 .
.