题目内容
(本题满分12分)
已知函数 ,且函数
,且函数 的图象关于直线
的图象关于直线 对称,又
对称,又 .
.
(1)求 的值域;
的值域;
(2)是否存在实数 ,使命题
,使命题 和
和 满足复合命题
满足复合命题 为真命题? 若存在, 求出
为真命题? 若存在, 求出 的范围; 若不存在, 说明理由.
的范围; 若不存在, 说明理由.
【答案】
(1)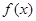 的值域为
的值域为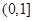 。
。
(2)存在实数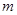 使得命题:
使得命题: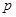 且
且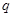 为真命题,且
为真命题,且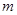 的取值范围为
的取值范围为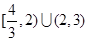 .
.
【解析】(1)由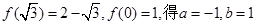 ,
,
于是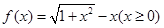 ------------------------------------3分
------------------------------------3分
由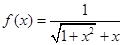 ,此函数在
,此函数在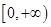 是单调减函数,
是单调减函数,
从而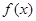 的值域为
的值域为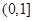 。------------------------------6分
。------------------------------6分
(2) 假定存在的实数m满足题设,即f(m2-m)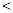 f(3m
f(3m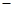 4)和
4)和 都成立
都成立
又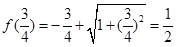 ∴
∴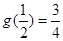 , ∴
, ∴ ---------8分
---------8分
由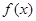 的值域为
的值域为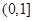 ,则
,则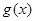 的定义域为
的定义域为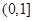
已证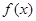 在
在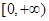 上是减函数,则
上是减函数,则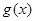 在
在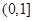 也是减函数,
也是减函数,
由减函数的定义得
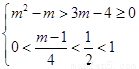 -------------------------------------------------11分
-------------------------------------------------11分
解得,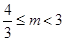 且
且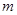 ≠
≠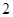 .
.
因此存在实数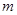 使得命题:
使得命题: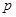 且
且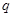 为真命题,且
为真命题,且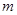 的取值范围为
的取值范围为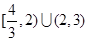 . ----12分
. ----12分

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面