题目内容
已知
（1）求f（0）和f[f（0）]的值；
（2）若f（x0）=3，求出x0所有可能取的值．
解：（1）∵0＜1，
，∴f（0）=3×0+2=2，
f[f（0）]=f（2）=22=4．
（2）当 x0＜1 时，3x0+2=3，∴
． 当 x0≥1 时，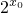
=3，x0=log23，
故x0所有可能取的值是
，或log23．
分析：（1）先求出 f（0）=2，故有f[f（0）]=f（2）=22．
（2）当 x0＜1 时，3x0+2=3，求得，当 x0≥1 时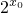，=3，求得 x0 的值．
点评：本题考查利用分段函数求函数的值的方法，体现了分类讨论的数学思想，分类讨论是解题的关键．
，∴f（0）=3×0+2=2，f[f（0）]=f（2）=22=4．
（2）当 x0＜1 时，3x0+2=3，∴
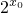． 当 x0≥1 时，=3，x0=log23，故x0所有可能取的值是
，或log23．分析：（1）先求出 f（0）=2，故有f[f（0）]=f（2）=22．
（2）当 x0＜1 时，3x0+2=3，求得
，当 x0≥1 时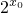，=3，求得 x0 的值．点评：本题考查利用分段函数求函数的值的方法，体现了分类讨论的数学思想，分类讨论是解题的关键．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
时，f（x）的最小值为2，求f（x）≥2成立的x的取值集合．
的值．
