题目内容
定义区间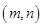 ,
,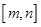 ,
,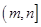 ,
,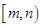 的长度均为
的长度均为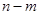 ,其中
,其中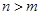 .
.
(1)求关于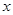 的不等式
的不等式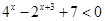 的解集构成的区间的长度;
的解集构成的区间的长度;
(2)若关于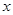 的不等式
的不等式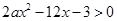 的解集构成的区间的长度为
的解集构成的区间的长度为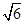 ,求实数
,求实数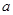 的值;
的值;
(3)已知关于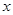 的不等式
的不等式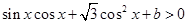 ,
,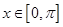 的解集构成的各区间的长度和超过
的解集构成的各区间的长度和超过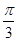 ,求实数
,求实数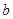 的取值范围.
的取值范围.
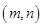 ,
,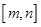 ,
,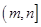 ,
,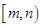 的长度均为
的长度均为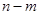 ,其中
,其中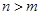 .
.(1)求关于
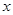 的不等式
的不等式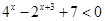 的解集构成的区间的长度;
的解集构成的区间的长度;(2)若关于
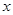 的不等式
的不等式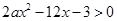 的解集构成的区间的长度为
的解集构成的区间的长度为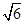 ,求实数
,求实数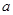 的值;
的值;(3)已知关于
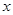 的不等式
的不等式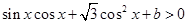 ,
,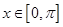 的解集构成的各区间的长度和超过
的解集构成的各区间的长度和超过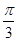 ,求实数
,求实数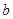 的取值范围.
的取值范围.(1)区间的长度是 .
.
(2) (
( 舍).
舍).
(3)实数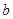 的取值范围是
的取值范围是 .
.
 .
.(2)
 (
( 舍).
舍).(3)实数
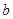 的取值范围是
的取值范围是 .
.试题分析:(1)不等式
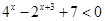 的解是
的解是
所以区间的长度是
 3分
3分(2)
当
 时,不符合题意 4分
时,不符合题意 4分当
 时,
时, 的两根设为
的两根设为 ,且
,且
结合韦达定理知

解得
 (
( 舍) 7分
舍) 7分(3)

=

设
 ,原不等式等价于
,原不等式等价于  ,
, 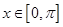 9分
9分因为函数
 的最小正周期是
的最小正周期是 ,
, 长度恰为函数的一个正周期
长度恰为函数的一个正周期所以
 时,
时, ,
, 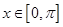 的解集构成的各区间的长度和超过
的解集构成的各区间的长度和超过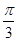
即实数
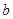 的取值范围是
的取值范围是 12分
12分点评:难题,指数不等式,常常化为同底数指数幂的不等关系或利用“换元法”,加以转化。三角函数不等式问题,通常利用三角公式进行化简,结合三角函数的图象和性质,加以处理,本题较难。

练习册系列答案
相关题目
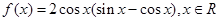 .
. 图像的对称中心;
图像的对称中心;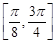 上的最小值和最大值.
上的最小值和最大值.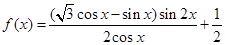 .
.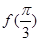 的值;
的值;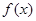 的最小正周期及单调递减区间.
的最小正周期及单调递减区间.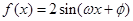 的图像如图所示,则
的图像如图所示,则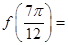 。
。
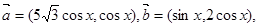 设函数
设函数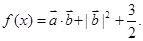 (Ⅰ)当
(Ⅰ)当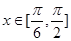 ,求函数
,求函数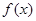 的值域;
的值域;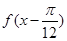 的值;
的值;
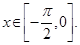
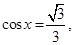 求函数
求函数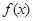 的值;
的值; ,在同一个周期内,当
,在同一个周期内,当 时
时 取最大值1,当
取最大值1,当 时,
时, ;
;  ;求在
;求在 内的所有实数根之和.
内的所有实数根之和.