题目内容
函数 在点
在点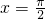 处连续,则实数k的值为
处连续,则实数k的值为
- A.

- B.

- C.1
- D.2
D
分析:利用罗比达法则求出 =
= ,函数在某处连续的定义可得 f(
,函数在某处连续的定义可得 f( )=log4k,由此求得实数k的值.
)=log4k,由此求得实数k的值.
解答:∵ =
= =
= =
= =
= =
= ,
,
函数 在点
在点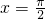 处连续,再由 f(
处连续,再由 f( )=log4k,以及函数在某处连续的定义可得log4k=
)=log4k,以及函数在某处连续的定义可得log4k= ,
,
解得 k=2.
故选D.
点评:本题主要考查函数在某处连续的定义,求函数在某处的极限的方法,罗比达法则的应用,属于基础题.
分析:利用罗比达法则求出
 =
= ,函数在某处连续的定义可得 f(
,函数在某处连续的定义可得 f( )=log4k,由此求得实数k的值.
)=log4k,由此求得实数k的值.解答:∵
 =
= =
= =
= =
= =
= ,
,函数
 在点
在点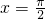 处连续,再由 f(
处连续,再由 f( )=log4k,以及函数在某处连续的定义可得log4k=
)=log4k,以及函数在某处连续的定义可得log4k= ,
,解得 k=2.
故选D.
点评:本题主要考查函数在某处连续的定义,求函数在某处的极限的方法,罗比达法则的应用,属于基础题.

练习册系列答案
相关题目
 在点x=1处连续,则实数a的值为( )
在点x=1处连续,则实数a的值为( )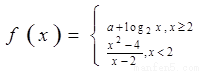 在点
在点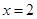 处连续,则常
处连续,则常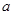 的值是
( )
的值是
( ) 2
2
 3
3
 4
4
 5
5