题目内容
已知函数
 .
.
(1)当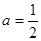 时,求
时,求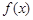 的单调区间;
的单调区间;
(2)若函数 在
在 单调递减,求实数
单调递减,求实数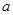 的取值范围.
的取值范围.
(1) 在
在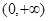 上单调递增.(2)
上单调递增.(2)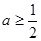 .
.
解析试题分析:(1)通过“求导数,求驻点,分区间讨论”,可得函数的单调区间.也可利用导数大于0或小于0 ,解不等式,得到单调区间.
(2)问题转化成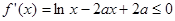 在
在 上恒成立,由
上恒成立,由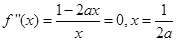 ,对
,对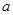 进行分类讨论,求得其范围.
进行分类讨论,求得其范围.
试题解析:(1)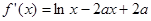 1分
1分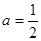 ,
,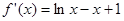 ,
,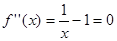 ,
,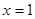 ,
,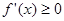 , 4分
, 4分 在
在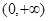 上单调递增 5 分
上单调递增 5 分
(2)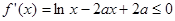 在
在 上恒成立,
上恒成立,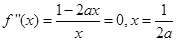
①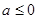 时,
时, 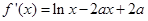 在
在 是增函数,其最小值为0,不合题意; 7分
是增函数,其最小值为0,不合题意; 7分
②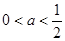 时,
时,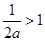 ,函数
,函数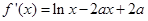 有最大值
有最大值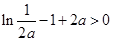 ,不合题意; 9分
,不合题意; 9分
③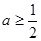 时,
时,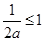 ,函数
,函数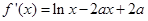 在
在 单调递增,在
单调递增,在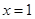 处取到最小值0; 11分
处取到最小值0; 11分
综上: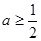 12分
12分
考点:应用导数研究函数的单调性、最值.

练习册系列答案
相关题目
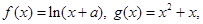 若函数
若函数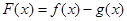 在x = 0处取得极值.
在x = 0处取得极值.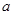 的值;
的值;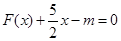 在区间[0,2]上恰有两个不同的实数根,求实数
在区间[0,2]上恰有两个不同的实数根,求实数 的取值范围;
的取值范围; 都成立.
都成立. .
. 时,求
时,求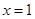 处的切线方程;
处的切线方程;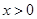 时,
时, ,求
,求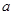 的取值范围.
的取值范围. 为圆心,
为圆心,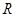 (
(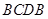 区域(阴影部分)用于种植学校观赏植物,
区域(阴影部分)用于种植学校观赏植物,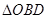 区域用于种植花卉出售,其余区域用于种植草皮出售.已知种植学校观赏植物的成本是每平方米20元,种植花卉的利润是每平方米80元,种植草皮的利润是每平方米30元.
区域用于种植花卉出售,其余区域用于种植草皮出售.已知种植学校观赏植物的成本是每平方米20元,种植花卉的利润是每平方米80元,种植草皮的利润是每平方米30元.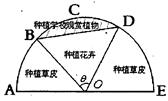
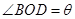 (单位:弧度),用
(单位:弧度),用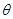 表示弓形
表示弓形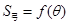 ;
;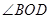 的大小才能使总利润最大?并求出该最大值.
的大小才能使总利润最大?并求出该最大值.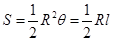 ,
,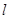 表示扇形的弧长)
表示扇形的弧长)
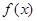 的图象关于原点对称,当
的图象关于原点对称,当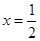 时,
时, ,求
,求 的解析式。
的解析式。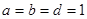 ,
,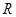 上的单调函数,求
上的单调函数,求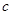 的取值范围
的取值范围

 的单调区间、最大值;
的单调区间、最大值; 的方程
的方程 的根的个数.
的根的个数. (
(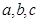 是常数)在
是常数)在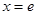 处的切线方程为
处的切线方程为 ,且
,且 .
.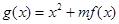 (
( )在区间
)在区间 内不是单调函数,求实数
内不是单调函数,求实数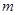 的取值范围;
的取值范围;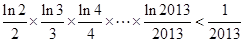 .
. .
.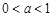 ,试讨论
,试讨论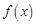 单调性;
单调性; ,当
,当 时,若
时,若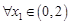 ,存在
,存在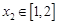 ,使
,使 ,求实数
,求实数 的
的
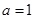 ,求
,求 的单调区间,
的单调区间,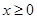 时,
时,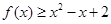 ,求
,求 的取值范围.
的取值范围.