题目内容
已知函数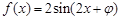 ,其中角
,其中角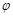 的终边经过点
的终边经过点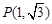 ,且
,且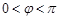 .
.
(1)求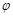 的值;
的值;
(2)求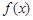 在
在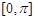 上的单调减区间.
上的单调减区间.
(1) (2)
(2)
解析试题分析:(1)这是由角的终边上点的坐标求角的大小的问题,可以通过作图用平面几何知识解决,也可由三角函数的定义,先求出这个角的某个三角函数值,再由角的终边所在的象限和角的范围去确定角的大小;(2)这是一个求函数 的单调区间的问题,从复合函数的角度出发可知解不等式
的单调区间的问题,从复合函数的角度出发可知解不等式 可得到函数的单调递减区间,再和区间
可得到函数的单调递减区间,再和区间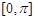 取交集即可.
取交集即可.
试题解析:(1) 角
角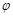 的终边经过点
的终边经过点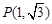 ,
, , 4分
, 4分
又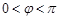 ,
, ; 7分
; 7分
(2)因为 ,由
,由 ,
,
得 ,
, , 11分
, 11分
取 ,则
,则 ,
, 在
在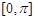 上的单调减区间为
上的单调减区间为 . 14分
. 14分
考点:三角函数的定义、 的单调性.
的单调性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
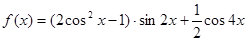 .
. 的最小正周期及最大值;
的最小正周期及最大值;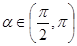 ,且
,且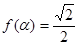 ,求
,求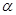 的值.
的值.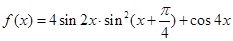 .
. 的最小正周期;
的最小正周期; 在
在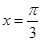 处取得最大值,求
处取得最大值,求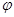 的值;
的值;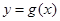 的单调递增区间.
的单调递增区间.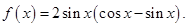
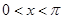 时,求
时,求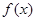 的最大值及相应的x值;
的最大值及相应的x值;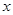 的图象经过怎样的变换得到f(x)的图象.
的图象经过怎样的变换得到f(x)的图象. 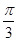 ,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.
,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.
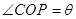 ,求
,求 面积的最大值及此时
面积的最大值及此时 的值.
的值. .
. 的最小正周期及最小值;
的最小正周期及最小值; 为锐角,且
为锐角,且 ,求
,求 ,
,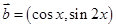 ,
, .
.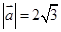 ,求
,求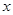 的值;
的值;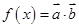 ,求
,求 的最大、最小值.
的最大、最小值. 为偶函数,周期为2
为偶函数,周期为2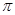 .
.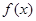 的解析式;
的解析式; 的值.
的值. 的部分图象如图所示.
的部分图象如图所示.
 的解析式;
的解析式; ,求
,求 的值.
的值.