Question

【题目】已知定义域为，对任意都有，且当时， .

(1)试判断的单调性，并证明；

(2)若，

①求的值；

②求实数的取值范围，使得方程有负实数根.

Answer 1

【答案】(1) 是上的减函数; （2）①; ②的取值范围

【解析】试题分析：（1）利用定义证明：任取，且，

， ， 下结论（2）①先赋值

求得，再令可解得②方程可化为，又单调，所以只需有负实数根.对进行分类讨论，分与两种情况.

试题解析：

解：（1）任取，且，

， ， 是上的减函数；

（2）①， ，

又，因为，

，

②方程可化为，又单调，所以只需有负实数根.记，

当时， ，解得，满足条件；

当时，函数图像是抛物线，且与轴的交点为（0，-1），方程有负实根包含两类情形：

①两根异号，即，解得；

②两个负实数根，即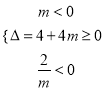，解得.

综上可得，实数的取值范围