题目内容
(本小题共14分)设函数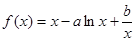 在
在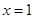 处取得极值.
处取得极值.
(Ⅰ)求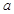 与
与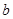 满足的关系式;
满足的关系式;
(Ⅱ)若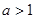 ,求函数
,求函数 的单调区间;
的单调区间;
(Ⅲ)若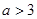 ,函数
,函数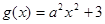 ,若存在
,若存在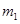 ,
,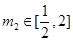 ,使得
,使得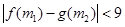 成立,求
成立,求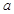 的取值范围.
的取值范围.
【答案】
解:(Ⅰ)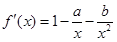 ,
…………………2分
,
…………………2分
由 得
得
 .
……………………3分
.
……………………3分
(Ⅱ)函数 的定义域为
的定义域为 ,
……………………4分
,
……………………4分
由(Ⅰ)可得 .
.
令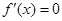 ,则
,则 ,
, .
……………………6分
.
……………………6分
因为 是
是 的极值点, 所以
的极值点, 所以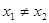 ,即
,即 . ……………………7分
. ……………………7分
所以当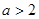 时,
时, ,
,
|
x |
|
1 |
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
↗ |
|
↘ |
|
↗ |
所以单调递增区间为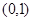 ,
, ,单调递减区间为
,单调递减区间为 .……………8分
.……………8分
当 时,
时, ,
,
所以单调递增区间为 ,
,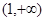 ,单调递减区间为
,单调递减区间为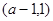 . ……………9分
. ……………9分
(Ⅲ)当 时,
时, 在
在 上为增函数,在
上为增函数,在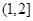 为减函数,
为减函数,
所以 的最大值为
的最大值为 .
……………………10分
.
……………………10分
因为函数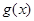 在
在 上是单调递增函数,
上是单调递增函数,
所以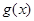 的最小值为
的最小值为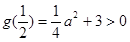 . ……………………11分
. ……………………11分
所以 在
在 上恒成立.
……………………12分
上恒成立.
……………………12分
要使存在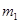 ,
,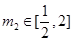 ,使得
,使得 成立,
成立,
只需要 ,即
,即 ,所以
,所以 .
………13分
.
………13分
又因为 , 所以
, 所以 的取值范围是
的取值范围是 . ……………………14分
. ……………………14分
【解析】略

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目



 (
( ).
). 时,求
时,求 的极值;
的极值; 时,求
时,求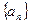 是正数组成的数列,其前
是正数组成的数列,其前 项和为
项和为 ,且对于所有的正整数
,且对于所有的正整数 .
. ,
, 的值;
的值; ,
, ,
, (
( ),求
),求 的前20项和
的前20项和 .
.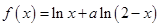 .
.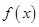 的定义域及其导数
的定义域及其导数 ;
;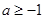 时,求函数
时,求函数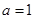 时,令
时,令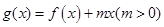 ,若
,若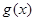 在
在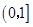 上的最大值为
上的最大值为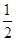 ,求实数
,求实数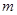 的值.
的值.