题目内容
【题目】已知![]() ,椭圆
,椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 长度的最大值为4.
长度的最大值为4.
(1)求![]() 的方程;
的方程;
(2)直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,当直线
,当直线![]() 变化(
变化(![]() 不与
不与![]() 轴重合)时,若
轴重合)时,若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由椭圆中弦长最长的位置在长轴位置可得![]() 的值,再由离心率并结合
的值,再由离心率并结合![]() 求得
求得![]() 的值,从而求得椭圆的标准方程;
的值,从而求得椭圆的标准方程;
(2)如图所示:

由题中关系式![]() 利用平面几何知识结合正弦定理可得:∠MPA=∠MPB,进而可得kPA=-kPB,设A点坐标
利用平面几何知识结合正弦定理可得:∠MPA=∠MPB,进而可得kPA=-kPB,设A点坐标![]() ,B点坐标
,B点坐标![]() ,M点坐标(
,M点坐标(![]() ,0)和直线l的方程
,0)和直线l的方程![]() ,和椭圆方程联立化简得
,和椭圆方程联立化简得![]() ,然后利用根的判别式、韦达定理和斜率公式综合运算可得
,然后利用根的判别式、韦达定理和斜率公式综合运算可得![]() 的值.
的值.
(1)由题意弦长AB长度的最大值为4,可得2a=4即得a=2,由离心率![]() ,
,
且![]() 联立解得
联立解得![]() =4,
=4, ![]() =3,所以椭圆
=3,所以椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
,![]() ,
,![]() 的方程为
的方程为![]() ,代入椭圆方程并整理得
,代入椭圆方程并整理得
![]() ,
,
由![]() ,
,
解得![]() ,
,
![]() ,
,![]() .
.
因为![]() 即
即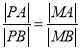 ,由角平分定理或正弦定理,即可得到
,由角平分定理或正弦定理,即可得到
![]() ,即
,即![]() ,所以
,所以![]() ,即
,即![]() ,
,
又![]() ,所以
,所以![]() ,
,
即![]() ,
,
所以![]() ,因为
,因为![]() 为变量,所以
为变量,所以![]() ,
,
所以点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
相关题目