题目内容
11.已知函数f(x)=$\left\{\begin{array}{l}{\frac{2+x}{x},x<0}\\{lo{g}_{2}\frac{1}{x},x>0}\end{array}\right.$,则f(x)+2≤0的解集为[-$\frac{2}{3}$,0)∪[4,+∞).分析 根据分段函数的表达式,结合分式不等式以及对数不等式的解法进行求解即可.
解答 解:若x<0,则由f(x)+2≤0得$\frac{2+x}{x}$+2≤0即2+x+2x≥0,得-$\frac{2}{3}$≤x<0,
若x>0,则由f(x)+2≤0得log2$\frac{1}{x}$+2≤0即-log2x≤-2,则log2x≥2,得x≥4,
综上不等式的解为-$\frac{2}{3}$≤x<0或x≥4,
故答案为:[-$\frac{2}{3}$,0)∪[4,+∞).
点评 本题主要考查不等式的求解,根据分段函数的表达式利用分类讨论的思想进行求解即可.

练习册系列答案
相关题目
1.给出下面的程序框图,则输出的结果为( )
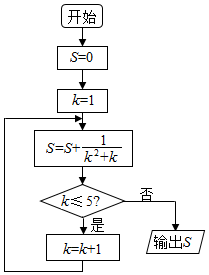

| A. | $\frac{5}{6}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{6}{7}$ |