题目内容
已知直线x-2y+2=0经过椭圆 的左顶点A和上顶点D,椭圆C的右顶点为B,点S是椭圆C上位于x轴上方的动点,直线AB,BS与直线
的左顶点A和上顶点D,椭圆C的右顶点为B,点S是椭圆C上位于x轴上方的动点,直线AB,BS与直线 分别交于M,N两点.
分别交于M,N两点.
(1)求椭圆C的方程;
(2)求线段MN的长度的最小值.
解:(1)由已知得,椭圆C的左顶点为A(-2,0),上顶点为D(0,1),
∴a=2,b=1,
故椭圆C的方程为 .
.
(2)直线AS的斜率k显然存在,且k>0,故可设直线AS的方程为y=k(x+2),从而 .
.
由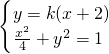 得(1+4k2)x2+16k2x+16k2-4=0.
得(1+4k2)x2+16k2x+16k2-4=0.
设S(x1,y1),则 得
得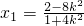 ,从而
,从而 .
.
即 ,又B(2,0)
,又B(2,0)
由 得
得 ,∴
,∴ ,
,
故 ,
,
又 ,∴
,∴ =
= .当且仅当
.当且仅当 ,即k=
,即k= 时等号成立
时等号成立
∴k= 时,线段MN的长度取最小值
时,线段MN的长度取最小值 .
.
分析:(1)由已知得,椭圆C的左顶点为A(-2,0),上顶点为D(0,1,由此能求出椭圆C的方程.
(2)设直线AS的方程为y=k(x+2),从而 .由题设条件可以求出
.由题设条件可以求出 ,所以
,所以 ,
,
再由均值不等式进行求解.
点评:本题考查椭圆与直线的位置关系,解题时要注意公式的灵活运用.
∴a=2,b=1,
故椭圆C的方程为
 .
.(2)直线AS的斜率k显然存在,且k>0,故可设直线AS的方程为y=k(x+2),从而
 .
.由
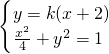 得(1+4k2)x2+16k2x+16k2-4=0.
得(1+4k2)x2+16k2x+16k2-4=0.设S(x1,y1),则
 得
得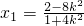 ,从而
,从而 .
.即
 ,又B(2,0)
,又B(2,0)由
 得
得 ,∴
,∴ ,
,故
 ,
,又
 ,∴
,∴ =
= .当且仅当
.当且仅当 ,即k=
,即k= 时等号成立
时等号成立∴k=
 时,线段MN的长度取最小值
时,线段MN的长度取最小值 .
.分析:(1)由已知得,椭圆C的左顶点为A(-2,0),上顶点为D(0,1,由此能求出椭圆C的方程.
(2)设直线AS的方程为y=k(x+2),从而
 .由题设条件可以求出
.由题设条件可以求出 ,所以
,所以 ,
,再由均值不等式进行求解.
点评:本题考查椭圆与直线的位置关系,解题时要注意公式的灵活运用.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
 已知直线x-2y+2=0经过椭圆
已知直线x-2y+2=0经过椭圆