Question

1．如图，在边长为a的正方形ABCD中，点E、F分别在边AD、CD上将，∠EBF=45°，求△EBF面积S的最小值．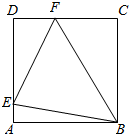

Answer 1

分析 设∠FBC=α，则∠EBA=45°-α，求出BF，BE，可得△EBF面积，化简，即可求△EBF面积S的最小值．

解答 解：设∠FBC=α，则∠EBA=45°-α，
∴BF=$\frac{a}{cosα}$，BE=$\frac{a}{cos（45°-α）}$，
∴S_△EBF=$\frac{1}{2}•BE•BF•sin45°$=$\frac{\sqrt{2}}{4}•\frac{{a}^{2}}{cosαcos（45°-α）}$=$\frac{{a}^{2}}{2}•\frac{1}{co{s}^{2}α-sinαcosα}$
=$\frac{{a}^{2}}{2}•\frac{1}{\frac{1}{2}+\frac{\sqrt{2}}{2}sin（45°-2α）}$≥${a}^{2}•\frac{1}{\sqrt{2}+1}$=$（\sqrt{2}-1）{a}^{2}$．
即△EBF面积S的最小值为：$（\sqrt{2}-1）{a}^{2}$．

点评 本题考查求△EBF面积S的最小值，考查三角函数知识的运用，正确表示△EBF面积S是关键．