Question

20．已知函数f（x）在区间[1，3]上连续不断，且f（1）f（2）f（3）＜0，则下列说法正确的是（　　）

• A． 函数f（x）在区间[1，2]或者[2，3]上有一个零点
• B． 函数f（x）在区间[1，2]、[2，3]上各有一个零点
• C． 函数f（x）在区间[1，3]上最多有两个零点
• D． 函数f（x）在区间[1，3]上有可能有2014个零点

Answer 1

分析 根据函数零点的判断得出①如果函数f（x）是单调函数，且f（1）＜0，f（2）＜0，f（3）＜0，f（x）就无零点，排除A，B
根据图形 判断C不正确，可得答案．

解答 解：函数f（x）在区间[1，3]上连续不断，且f（1）f（2）f（3）＜0，
①如果函数f（x）是单调函数，且f（1）＜0，f（2）＜0，f（3）＜0，
f（x）就无零点，
故：A，B不正确．
②如果函数f（x）不是单调函数，且f（1）＜0，f（2）＜0，f（3）＜0，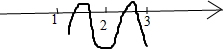

根据图形可知函数f（x）在区间[1，3]上有4个零点，
故：C不正确．
所以排除：A，B，C
故选：D．

点评 本题考查了函数零点的判断方法，考虑全面，结合图形判断求解，属于中档题．