题目内容
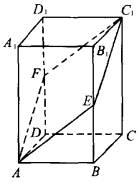
 如图所示,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC
如图所示,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC(1)求异面直线BE、AB1所成的角的大小;
(2)求A1到截面BDE的距离;
(3)求二面角A1-DE-B的大小.
分析:以DA,DC,DD1分别为x轴,y轴,z轴,建立空间直角坐标系D-xyz.
(1)先求得
=(-2,0,1),
=(0,2,4),利用向量的夹角求异面直线BE、AB1所成的角.
(2)根据空间直角坐标系个点坐标,即向量垂直计算,可得A1C⊥BD,A1C⊥DE又DB∩DE=D即可得A1C⊥平面DBE
,再利用等体积可求.
(3)由(2)知向量
为平面DBE的一个法向量,根据向量坐标计算,即可得到二面角A1-DE-B的余弦值.
(1)先求得
| BE |
| AB1 |
(2)根据空间直角坐标系个点坐标,即向量垂直计算,可得A1C⊥BD,A1C⊥DE又DB∩DE=D即可得A1C⊥平面DBE
,再利用等体积可求.
(3)由(2)知向量
| A1C |
解答:解:以DA,DC,DD1分别为x轴,y轴,z轴,建立空间直角坐标系D-xyz.
则D(0,0,0),B(2,2,0),C(0,2,0),E(0,2,1),A1(2,0,4),A(2,0,0),B1(2,2,4),
=(0,2,1),
=(2,2,0),
=(-2,2,-4),
=(2,0,4)
(1)
=(-2,0,1),
=(0,2,4)
设异面直线BE、AB1所成的角的大小为α,则cosα=
=
,
∴α=arccos
(2)证明:∵
•
=-4+4+0=0,
•
=0+4-4=0,
∴A1C⊥BD,A1C⊥DE
又DB∩DE=D,∴A1C⊥平面DBE
设C到截面BDE的距离为h,则有
∵VC-BDE=VE-BCD,∴h=
∵A1C=2
∴A1到截面BDE的距离为
;
(3)由(2)知向量
为平面DBE的一个法向量
设平面DA1E的法向量n=(x,y,z)
由 n⊥
,n⊥
得2y+z=0,2x+4z=0
令z=-2,得x=4,y=1,
∴n=(4,1,-2)
又二面角A1-DE-B为锐角
∴二面角A1-DE-B的余弦值为
则D(0,0,0),B(2,2,0),C(0,2,0),E(0,2,1),A1(2,0,4),A(2,0,0),B1(2,2,4),
| DE |
| DB |
| A1C |
| DA1 |
(1)
| BE |
| AB1 |
设异面直线BE、AB1所成的角的大小为α,则cosα=
| 4 | ||||
|
| 2 |
| 5 |
∴α=arccos
| 2 |
| 5 |
(2)证明:∵
| A1C |
| DB |
| A1C |
| DE |
∴A1C⊥BD,A1C⊥DE
又DB∩DE=D,∴A1C⊥平面DBE
设C到截面BDE的距离为h,则有
∵VC-BDE=VE-BCD,∴h=
| ||
| 6 |
∵A1C=2
| 6 |
∴A1到截面BDE的距离为
11
| ||
| 6 |
(3)由(2)知向量
| A1C |
设平面DA1E的法向量n=(x,y,z)
由 n⊥
| DE |
| DA1 |
令z=-2,得x=4,y=1,
∴n=(4,1,-2)
又二面角A1-DE-B为锐角
∴二面角A1-DE-B的余弦值为
| ||
| 42 |
点评:本题以正四棱柱为载体,考查线线角,面面角,考查利用空间向量解决立体几何问题,计算要小心.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
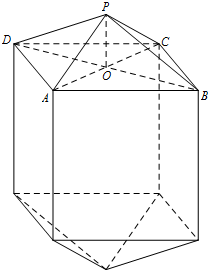 某公司拟制造如图所示的工件(长度单位:米),要求工件的体积为10立方米,其中工件的中间为长方体,上下两端为相同的正四棱锥,其底面边长AB=a,高PO=
某公司拟制造如图所示的工件(长度单位:米),要求工件的体积为10立方米,其中工件的中间为长方体,上下两端为相同的正四棱锥,其底面边长AB=a,高PO= 一个三棱柱恰好可放入一个正四棱柱的容体中,底面如图所示,其中三棱柱的底面AEF是一个直角三角形,∠AEF=90°,AE=a,EF=b,三棱柱的高与正四棱柱的高均为1,则此正四棱柱的体积为
一个三棱柱恰好可放入一个正四棱柱的容体中,底面如图所示,其中三棱柱的底面AEF是一个直角三角形,∠AEF=90°,AE=a,EF=b,三棱柱的高与正四棱柱的高均为1,则此正四棱柱的体积为