题目内容
如图，海平面上的甲船位于中心O的南偏西30°，与O相距10海里的C处，现甲船以30海里/小时的速度沿直线CB去营救位于中心O正东方向20海里的B处的乙船，甲船需要 小时到达B处．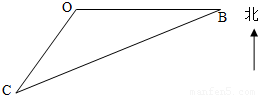
【答案】分析：先根据余弦定理求出CB的长度，再除以速度可得时间．
解答：解：由题意，对于CB的长度可用余弦定理求解，
得CB2=CO2+OB2-|CO||OB|cos120°=100+400+200=700，
因此|CB|=10
，因此甲船需要的时间为
=
（小时）．
故答案为：
点评：本题主要考查余弦定理的应用．属基础题．
解答：解：由题意，对于CB的长度可用余弦定理求解，
得CB2=CO2+OB2-|CO||OB|cos120°=100+400+200=700，
因此|CB|=10
，因此甲船需要的时间为=（小时）．故答案为：
点评：本题主要考查余弦定理的应用．属基础题．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
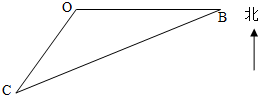如图，海平面上的甲船位于中心O的南偏西30°，与O相距10海里的C处，现甲船以30海里/小时的速度沿直线CB去营救位于中心O正东方向20海里的B处的乙船，甲船需要
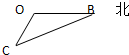如图，海平面上的甲船位于中心O的南偏西30°与O相距10海里的C处用船只以30海里/小时的速度沿直线CB营救位于中心O正东方向20海里的B处的乙船，甲船到达B处需要（ ）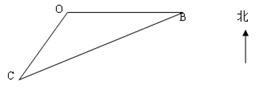
，与O相距10海里的C处，现甲船以30海里/小时的速度沿直线CB去营救位于中心O正东方向20海里的B处的乙船，甲船需要 小时到达B处.
小时．