题目内容
已知抛物线x2=4y的焦点为F,A、B是抛物线上的两动点,且(Ⅰ)证明![]() ·
·![]() 为定值;
为定值;
(Ⅱ)设△ABM的面积为S,写出S=f(λ)的表达式并求S的最小值.
解:(Ⅰ)F(0,1),λ>0,设A(x1,y1),B(x2,y2),由![]() =λ
=λ![]() 得
得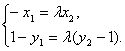
∴![]() =λ2
=λ2![]() ,并把y1=
,并把y1=![]()
![]() y2=
y2=![]()
![]() 代入得:
代入得:
y1=λ2y2.由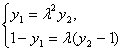
![]() y1=λ,y2=
y1=λ,y2=![]() ,且有x1x2=-λ
,且有x1x2=-λ![]() =-4λy2=-4.
=-4λy2=-4.
由y=![]() x2得,y′=
x2得,y′=![]() x过A、B两点的切线方程分别为:
x过A、B两点的切线方程分别为:
y=![]() x1(x-x1)+y1,y=
x1(x-x1)+y1,y=![]() x2(x-x2)+y2.
x2(x-x2)+y2.
即:y=![]() x1x-
x1x-![]()
![]() ;y=
;y=![]() x2x-
x2x-![]()
![]() .
.
解出交点M的坐标为(![]() ,
,![]() )=(
)=(![]() ,-1).
,-1).
∴![]() ·
·![]() =(
=(![]() ,-2)·(x2-x1,y2-y1)=
,-2)·(x2-x1,y2-y1)=![]() (
(![]() -
-![]() )-2(
)-2(![]()
![]() -
-![]()
![]() )=0.
)=0.
(Ⅱ)由(Ⅰ)知在△ABM中,FM⊥AB,因而S=![]() |AB||FM|,
|AB||FM|,
|FM|=![]() +
+![]() ,
,
|AB|=|AF|+|FB|=y1+y2+2=λ+![]() +2=(
+2=(![]() +
+![]() )2,
)2,
∴S=![]() (
(![]() +
+![]() )3.∵
)3.∵![]() +
+![]() ≥2,
≥2,
∴S≥4,当且仅当λ=1时,S最小值4.

练习册系列答案
相关题目
 已知抛物线x2=4y上的点P(非原点)处的切线与x轴,y轴分别交于Q,R两点,F为焦点.
已知抛物线x2=4y上的点P(非原点)处的切线与x轴,y轴分别交于Q,R两点,F为焦点. (2009•温州一模)如图,已知抛物线x2=4y,过抛物线上一点A(x1,y1)(不同于顶点)作抛物线的切线l,并交x轴于点C,在直线y=-1上任取一点H,过H作HD垂直x轴于D,并交l于点E,过H作直线HF垂直直线l,并交x轴于点F.
(2009•温州一模)如图,已知抛物线x2=4y,过抛物线上一点A(x1,y1)(不同于顶点)作抛物线的切线l,并交x轴于点C,在直线y=-1上任取一点H,过H作HD垂直x轴于D,并交l于点E,过H作直线HF垂直直线l,并交x轴于点F. (2011•浙江模拟)已知抛物线x2=4y,圆C:x2+(y-2)2=4,M(x0,y0),(x0>0,y0>0)为抛物线上的动点.
(2011•浙江模拟)已知抛物线x2=4y,圆C:x2+(y-2)2=4,M(x0,y0),(x0>0,y0>0)为抛物线上的动点.