题目内容
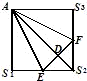如图在正方形AS1S2S3中，E、F分别是边S1S2、S2S3的中点，D是EF的中点，沿AE、EF、AF把这个正方形折成一个几何体，使三点S1、S2、S3重合于一点S，下面有5个结论：①AS⊥平面SEF；②AD⊥平面SEF；③SF⊥平面AEF；④EF⊥平面SAD；⑤SD⊥平面AEF．其中正确的是
- A.①③
- B.②⑤
- C.①④
- D.②④
C
分析：对于①④利用直线与平面垂直的判定定理进行证明，对于②③⑤利用反证法进行证明，假设成立，然后找出矛盾，得到结论．
解答：∵AS⊥SE，AS⊥SF，SE∩SF=S
∴AS⊥平面SEF故①正确
假设AD⊥平面SEF，而AS⊥平面SEF
则AS∥AD，而AS与AD相交，矛盾，故②不正确
假设SF⊥平面AEF，则SF⊥EF
而SF与EF成45°角，矛盾，故③不正确
∵EF⊥AD，EF⊥SD，而AD∩SD=D
∴EF⊥平面SAD，故④正确
假设SD⊥平面AEF，则SD⊥AD，而AS⊥SD
则AD∥AS，而AS与AD相交，矛盾，故⑤不正确
故选C
点评：本题主要考查了直线与平面垂直的判定，同时考查了空间想象能力、运算能力和推理论证能力，属于基础题．
分析：对于①④利用直线与平面垂直的判定定理进行证明，对于②③⑤利用反证法进行证明，假设成立，然后找出矛盾，得到结论．
解答：∵AS⊥SE，AS⊥SF，SE∩SF=S
∴AS⊥平面SEF故①正确
假设AD⊥平面SEF，而AS⊥平面SEF
则AS∥AD，而AS与AD相交，矛盾，故②不正确
假设SF⊥平面AEF，则SF⊥EF
而SF与EF成45°角，矛盾，故③不正确
∵EF⊥AD，EF⊥SD，而AD∩SD=D
∴EF⊥平面SAD，故④正确
假设SD⊥平面AEF，则SD⊥AD，而AS⊥SD
则AD∥AS，而AS与AD相交，矛盾，故⑤不正确
故选C
点评：本题主要考查了直线与平面垂直的判定，同时考查了空间想象能力、运算能力和推理论证能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
，则y=f（x）的图象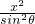
-
=1（0＜θ≤
，b＞0）的两个焦点，过F1的直线交双曲线的同支于A、B两点，如果|AB|=m，则△AF2B的周长的最大值是
}，其中
=（2x-2b，1），
=（1，1+2b）为向量，点列Pn（an，bn）在点集L中，P1为L的轨迹与y轴的交点，已知数列{an}为等差数列，且公差为1，3．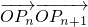
的最小值；（其中O为坐标原点）
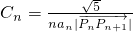（n≥2），求：C2+C3+…+Cn的值．
，若f（x）在[-2，2]上的最大值，最小值分别为M，N，则M+N=________．