题目内容
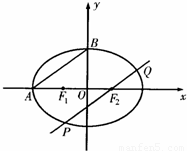
如图所示,F1、F2分别为椭圆C: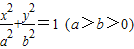 的左、右两个焦点,A、B为两个顶点,已知椭圆C上的点
的左、右两个焦点,A、B为两个顶点,已知椭圆C上的点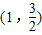 到F1、F2两点的距离之和为4.
到F1、F2两点的距离之和为4.(Ⅰ)求椭圆C的方程;
(Ⅱ)过椭圆C的焦点F2作AB的平行线交椭圆于P、Q两点,求△F1PQ的面积.
【答案】分析:(Ⅰ)由题设知:2a=4,即a=2,将点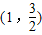 代入椭圆方程得
代入椭圆方程得 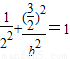 ,解得b2=3,由此能得到椭圆方程.
,解得b2=3,由此能得到椭圆方程.
(Ⅱ)由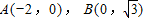 ,知
,知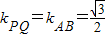 ,所以PQ所在直线方程为
,所以PQ所在直线方程为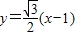 ,由
,由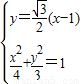 得
得 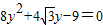 ,设P (x1,y1),Q (x2,y2),由韦达定理能导出
,设P (x1,y1),Q (x2,y2),由韦达定理能导出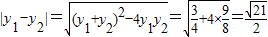 ,由此能求出△F1PQ的面积.
,由此能求出△F1PQ的面积.
解答:解:(Ⅰ)由题设知:2a=4,即a=2
将点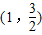 代入椭圆方程得
代入椭圆方程得 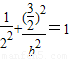 ,解得b2=3
,解得b2=3
∴c2=a2-b2=4-3=1,故椭圆方程为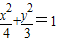 --------------(3分)
--------------(3分)
(Ⅱ)由(Ⅰ)知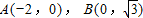 ,∴
,∴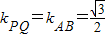 ,
,
∴PQ所在直线方程为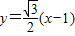 ---------------(5分)
---------------(5分)
由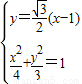 得
得 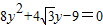 ---------------------------------(7分)
---------------------------------(7分)
设P (x1,y1),Q (x2,y2),则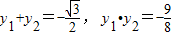 --------(8分)
--------(8分)
∴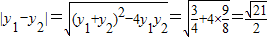 --------------------------(9分)
--------------------------(9分)
∴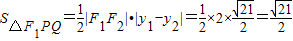 .-------------------------(10分)
.-------------------------(10分)
点评:本题考查椭圆C的方程和求△F1PQ的面积.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
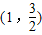 代入椭圆方程得
代入椭圆方程得 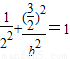 ,解得b2=3,由此能得到椭圆方程.
,解得b2=3,由此能得到椭圆方程.(Ⅱ)由
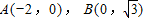 ,知
,知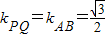 ,所以PQ所在直线方程为
,所以PQ所在直线方程为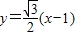 ,由
,由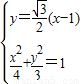 得
得 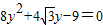 ,设P (x1,y1),Q (x2,y2),由韦达定理能导出
,设P (x1,y1),Q (x2,y2),由韦达定理能导出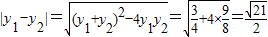 ,由此能求出△F1PQ的面积.
,由此能求出△F1PQ的面积.解答:解:(Ⅰ)由题设知:2a=4,即a=2
将点
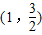 代入椭圆方程得
代入椭圆方程得 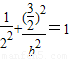 ,解得b2=3
,解得b2=3∴c2=a2-b2=4-3=1,故椭圆方程为
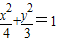 --------------(3分)
--------------(3分)(Ⅱ)由(Ⅰ)知
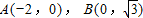 ,∴
,∴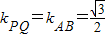 ,
,∴PQ所在直线方程为
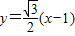 ---------------(5分)
---------------(5分)由
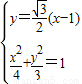 得
得 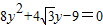 ---------------------------------(7分)
---------------------------------(7分)设P (x1,y1),Q (x2,y2),则
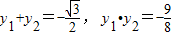 --------(8分)
--------(8分)∴
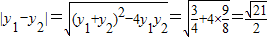 --------------------------(9分)
--------------------------(9分)∴
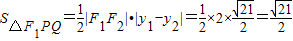 .-------------------------(10分)
.-------------------------(10分)点评:本题考查椭圆C的方程和求△F1PQ的面积.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 如图所示,F1,F2分别为椭圆C:
如图所示,F1,F2分别为椭圆C: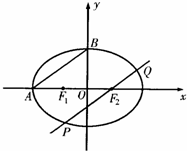 如图所示,F1、F2分别为椭圆C:
如图所示,F1、F2分别为椭圆C: 如图所示,F1、F2分别为椭圆C:
如图所示,F1、F2分别为椭圆C: 如图所示,F1、F2分别为椭圆C:
如图所示,F1、F2分别为椭圆C: (2013•牡丹江一模)如图所示,F1和F2分别是双曲线
(2013•牡丹江一模)如图所示,F1和F2分别是双曲线