题目内容
【题目】某社区![]() 名居民参加
名居民参加![]() 年国庆活动,他们的年龄在
年国庆活动,他们的年龄在![]() 岁至
岁至![]() 岁之间,将年龄按
岁之间,将年龄按![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分组,得到的频率分布直方图如图所示.
分组,得到的频率分布直方图如图所示.
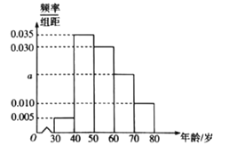
(1)求![]() 的值,并求该社区参加
的值,并求该社区参加![]() 年国庆活动的居民的平均年龄(每个分组取中间值作代表);
年国庆活动的居民的平均年龄(每个分组取中间值作代表);
(2)现从年龄在![]() 、
、![]() 的人员中按分层抽样的方法抽取
的人员中按分层抽样的方法抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人进行座谈,用
人进行座谈,用![]() 表示参与座谈的居民的年龄在
表示参与座谈的居民的年龄在![]() 的人数,求
的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)若用样本的频率代替概率,用随机抽样的方法从该地![]() 岁至
岁至![]() 岁之间的市民中抽取
岁之间的市民中抽取![]() 名进行调查,其中有
名进行调查,其中有![]() 名市民的年龄在
名市民的年龄在![]() 的概率为
的概率为![]() ,当
,当![]() 最大时,求
最大时,求![]() 的值.
的值.
【答案】(1)![]() ,平均年龄
,平均年龄![]() ;(2)分布列见解析,
;(2)分布列见解析,![]() ;(3)
;(3)![]() .
.
【解析】
(1)由频率分布直方图中所有矩形面积之和为![]() ,求出
,求出![]() 的值,再将所有矩形底边中点值乘以矩形面积,再将所得的数相加即可得出该社区
的值,再将所有矩形底边中点值乘以矩形面积,再将所得的数相加即可得出该社区![]() 年国庆活动的居民的平均年龄;
年国庆活动的居民的平均年龄;
(2)先根据分层抽样得知,所抽取的![]() 人中,年龄在
人中,年龄在![]() 的抽取
的抽取![]() 人、年龄在
人、年龄在![]() 的抽取
的抽取![]() 人,可得出随机变量
人,可得出随机变量![]() 的可能取值为
的可能取值为![]() 、
、![]() 、
、![]() ,并利用古典概型的概率公式计算出随机变量
,并利用古典概型的概率公式计算出随机变量![]() 分别取
分别取![]() 、
、![]() 、
、![]() 时的概率,列出随机变量
时的概率,列出随机变量![]() 的分布列,并利用数学期望公式计算出随机变量
的分布列,并利用数学期望公式计算出随机变量![]() 的数学期望;
的数学期望;
(3)设年龄在![]() 的人数为
的人数为![]() ,可知
,可知![]() ,利用独立重复试验的概率公式得出
,利用独立重复试验的概率公式得出![]() ,分析出数列
,分析出数列![]() 的单调性,可求出
的单调性,可求出![]() 的最大值及对应的
的最大值及对应的![]() 的值.
的值.
(1)由频率分布直方图知![]() ,解得
,解得![]() ,
,
所以该社区参加![]() 年国庆活动的居民的平均年龄为
年国庆活动的居民的平均年龄为
![]()
![]() ;
;
(2)年龄在![]() 的人数为
的人数为![]() ,年龄在
,年龄在![]() 的人数为
的人数为![]() .
.
根据分层抽样,可知年龄在![]() 的抽取
的抽取![]() 人、年龄在
人、年龄在![]() 的抽取
的抽取![]() 人.
人.
所以![]() 的可能取值为0,1,2,且
的可能取值为0,1,2,且![]() ,
,![]() ,
,![]() ,
,
所以![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
所以![]() ;
;
(3)由题可知年龄在![]() 内的频率为
内的频率为![]() .
.
设年龄在![]() 的人数为
的人数为![]() ,所以
,所以![]() .
.
![]() .
.
设
![]() ,
,
由![]() 得
得![]() ,此时
,此时![]() ;由
;由![]() 得
得![]() ,此时
,此时![]() .
.
所以当![]() 时,
时,![]() 最大.
最大.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案【题目】从2016年到2019年的某城市方便面销量情况如图所示:
年份 | 2016 | 2017 | 2018 | 2019 |
时间代号 | 1 | 2 | 3 | 4 |
年销量 | 462 | 444 | 404 | 385 |
(1)根据上表,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .用所求回归方程预测2020年(
.用所求回归方程预测2020年(![]() )方便面在该城市的年销量;
)方便面在该城市的年销量;
(2)某媒体记者随机对身边的10位朋友做了一次调查,其中3位受访者认为方便面是健康食品.现从这10人中抽取3人进行深度访谈,记![]() 表示随机抽取的3人认为方便面是健康食品的人数,求随机变量
表示随机抽取的3人认为方便面是健康食品的人数,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
参考公式:回归方程:![]() ,其中
,其中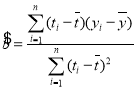 ,
,![]() .
.
参考数据:![]() .
.