题目内容
已知映射f:(a,b)→(x1x2,|x1-x2|),其中x1,x2(x1,x2∈C)是方程x2+ax+b=0(a,b∈R)的两根,则(2,1)的像为分析:先求出映射f:(a,b)→( b,
),令a=2,b=1 可得(2,1)的像; 由
可得
,可得(2,1)的原像.
| a2-4b |
|
|
解答:解:由题意可得 x1+x2=-a,x1•x2=b,|x1-x2|=
=
,
故映射f:(a,b)→(b,|x1-x2|),即映射f:(a,b)→( b,
),
令a=2,b=1 可得 (2,1)的像( b,
)=(1,0).
由
可得
,故(2,1)的原像为 (±3,2).
故答案为 (1,0),(±3,2).
| (x1+ x2) 2-4x1x2 |
| a2-4b |
故映射f:(a,b)→(b,|x1-x2|),即映射f:(a,b)→( b,
| a2-4b |
令a=2,b=1 可得 (2,1)的像( b,
| a2-4b |
由
|
|
故答案为 (1,0),(±3,2).
点评:本题考查映射的定义,像和原像的定义,求出映射f:(a,b)→( b,
),是解题的关键.
| a2-4b |

练习册系列答案
相关题目
已知映射f:A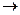 B, A=B=R,对应法则f:x
B, A=B=R,对应法则f:x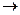 y = –x2+2x,对于实数k
y = –x2+2x,对于实数k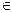 B在A中没有原象,则k的取值范围是 ( )
B在A中没有原象,则k的取值范围是 ( )
| A.k>1 | B.k≥1 | C.k<1 | D.k≤2 |
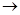 B, A=B=R,对应法则f:x
B, A=B=R,对应法则f:x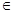 B在A中没有原象,则k的取值范围是
( )
B在A中没有原象,则k的取值范围是
( )