题目内容
已知一条曲线上的点到定点O(0,0)的距离是到定点A(3,0)距离的二倍,求这条曲线的方程.
分析:设M(x,y)是曲线上任意的一点,点M在曲线上的条件是|MO|=2|MA|,利用两点间距离公式,能求出这条曲线方程.
解答:解:设M(x,y)是曲线上任意的一点,
∵曲线上的点到定点O(0,0)的距离是到定点A(3,0)距离的二倍,
∴点M在曲线上的条件是|MO|=2|MA|.(4分)
由两点间距离公式,
得
=2
,
两边平方并化简得x2-8x+y2+12=0.
故这条曲线的方程为x2-8x+y2+12=0.(10分)
∵曲线上的点到定点O(0,0)的距离是到定点A(3,0)距离的二倍,
∴点M在曲线上的条件是|MO|=2|MA|.(4分)
由两点间距离公式,
得
| x2+y2 |
| (x-3)2+y2 |
两边平方并化简得x2-8x+y2+12=0.
故这条曲线的方程为x2-8x+y2+12=0.(10分)
点评:本题考查曲线方程的求法,解题时要认真审题,仔细解答,注意两点间距离公式的合理运用.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
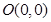 的距离是到定点
的距离是到定点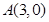 距离的二倍,求这条曲线的方程.
距离的二倍,求这条曲线的方程. 的距离是到定点
的距离是到定点 距离的二倍,求这条曲线的方程.
距离的二倍,求这条曲线的方程.