题目内容
17. 已知三次函数f(x)=ax3+bx2+cx+d的图象如图所示,则$\frac{f′(-2)}{f′(1)}$=( )
已知三次函数f(x)=ax3+bx2+cx+d的图象如图所示,则$\frac{f′(-2)}{f′(1)}$=( )| A. | 5 | B. | -5 | C. | 2 | D. | -2 |
分析 根据函数导数和极值之间的关系,求出对应a,b,c的关系,即可得到结论.
解答 解:由三次函数的图象可知,x=2函数的极大值,x=-1是极小值,
即2,-1是f′(x)=0的两个根,
∵f(x)=ax3+bx2+cx+d,
∴f′(x)=3ax2+2bx+c,
由f′(x)=3ax2+2bx+c=0,
得2+(-1)=-$\frac{2b}{3a}$=1,
-1×2=$\frac{c}{3a}$=-2,
即c=-6a,2b=-3a,
即f′(x)=3ax2+2bx+c=3ax2-3ax-6a=3a(x-2)(x+1),
则f′(-2)=3a(-2-2)(-2+1)=12a,
f′(1)=3a(1-2)(1+1)=-6a,
∴$\frac{f′(-2)}{f′(1)}$=$\frac{12a}{-6a}$=-2,
故选:D.
点评 本题主要考查函数的极值和导数之间的关系,以及根与系数之间的关系的应用,考查学生的计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
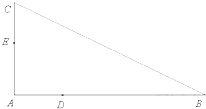 如图,△ABC中∠A=90°,D,E分别为边AB,AC上的点,且不与△ABC的顶点重合.已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x+mn=0的两个根.
如图,△ABC中∠A=90°,D,E分别为边AB,AC上的点,且不与△ABC的顶点重合.已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x+mn=0的两个根.