题目内容
已知函数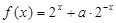 是定义域为
是定义域为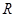 的奇函数,(1)求实数
的奇函数,(1)求实数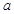 的值;(2)证明
的值;(2)证明 是
是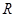 上的单调函数;(3)若对于任意的
上的单调函数;(3)若对于任意的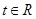 ,不等式
,不等式 恒成立,求
恒成立,求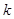 的取值范围。
的取值范围。
【答案】
(1)∵ 是定义域为
是定义域为 的奇函数,
的奇函数,
∴ ,∴
,∴ ,……………(3分)
,……………(3分)
经检验当 时,
时, 是奇函数,故所求
是奇函数,故所求 。……………(4分)
。……………(4分)
(2) ,
, ,且
,且 ,
,
 ……………(6分)
……………(6分)
∵ ,∴
,∴ ,即
,即 ∴
∴ 即
即 ,
,
∴ 是
是 上的递增函数,即
上的递增函数,即 是
是 上的单调函数。……………(8分)
上的单调函数。……………(8分)
(3)∵根据题设及(2)知
 ,……………(10分)
,……………(10分)
∴原不等式恒成立即是 在
在 上恒成立,∴
上恒成立,∴ ,…(11分)
,…(11分)
∴所求 的取值范围是
的取值范围是
【解析】略

练习册系列答案
相关题目
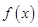 是定义域为
是定义域为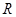 的单调减函数,且是奇函数,当
的单调减函数,且是奇函数,当 时,
时,
 的不等式
的不等式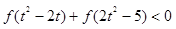
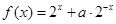 是定义域为
是定义域为 的奇函数,(1)求实数
的奇函数,(1)求实数 的值;(2)证明
的值;(2)证明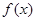 是
是 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围. 是定义域为
是定义域为 的奇函数,且当
的奇函数,且当 时,
时,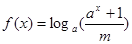 ,(
,( 。
。 的值;并求函数
的值;并求函数
 上是增函数。
上是增函数。 是定义域为
是定义域为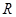 的偶函数,且在
的偶函数,且在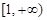 上单调递增,则不等式
上单调递增,则不等式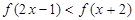 的解集为( )
的解集为( ) B.
B.
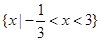 D.
D.