题目内容
已知函数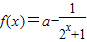 为奇函数.
为奇函数.(1)求a的值;
(2)求函数f(x)的值域.
【答案】分析:(1)由已知函数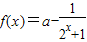 为奇函数,则f(1)+f(-1)=0,由此构造关于a的方程,解方程可得答案.
为奇函数,则f(1)+f(-1)=0,由此构造关于a的方程,解方程可得答案.
(2)根据(1)可得函数的解析式,结合指数的性质,利用分析法可得函数f(x)的值域
解答:解:(1)f(x)为奇函数,
∴f(1)+f(-1)=0,
得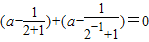 ,
,
∴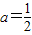 ,…(3分)
,…(3分)
此时,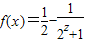 ,
,
即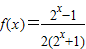 ,
,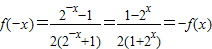
即f(x)为奇函数.
∴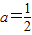 .…(6分)
.…(6分)
(或f(x)+f(-x)=0,即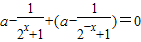 ,∴
,∴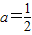 )
)
(2)由(1)知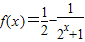 ,
,
∵2x+1>1,
∴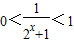 ,
,
∴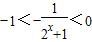 ,
,
所以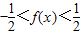 ,
,
所以f(x)的值域为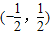 .…(12分)
.…(12分)
点评:本题考查的知识点是函数奇偶性的性质,函数的值域,其中求出函数的解析式是解答的关键.
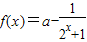 为奇函数,则f(1)+f(-1)=0,由此构造关于a的方程,解方程可得答案.
为奇函数,则f(1)+f(-1)=0,由此构造关于a的方程,解方程可得答案.(2)根据(1)可得函数的解析式,结合指数的性质,利用分析法可得函数f(x)的值域
解答:解:(1)f(x)为奇函数,
∴f(1)+f(-1)=0,
得
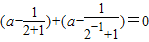 ,
,∴
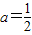 ,…(3分)
,…(3分)此时,
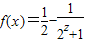 ,
,即
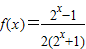 ,
,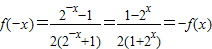
即f(x)为奇函数.
∴
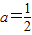 .…(6分)
.…(6分)(或f(x)+f(-x)=0,即
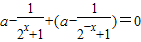 ,∴
,∴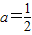 )
)(2)由(1)知
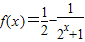 ,
,∵2x+1>1,
∴
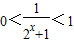 ,
,∴
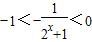 ,
,所以
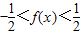 ,
,所以f(x)的值域为
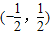 .…(12分)
.…(12分)点评:本题考查的知识点是函数奇偶性的性质,函数的值域,其中求出函数的解析式是解答的关键.

练习册系列答案
相关题目
 为奇函数,
为奇函数, 为偶函数,且
为偶函数,且 .
. ,则称
,则称 是函数
是函数 为奇函数,
为奇函数, 为偶函数
为偶函数 ,且
,且 .
. ,则称
,则称 是函数
是函数